Норберт Винер - Кибернетика или управление и связь в животном и машине

Входящую в это выражение константу можно определить из соотношения

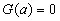, (3.61)

или

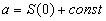. (3.62)

Очевидно, что если а конечно, то безразлично, какое значение мы ему дадим; в самом деле, наш оператор не [c.141]изменится от прибавления одной и той же величины ко всем значениям λ. Поэтому можно взять а =0. Таким образом, мы определили λ как функцию от G и, следовательно, G — как функцию от λ. Из (3.55) следует, что мы тем самым определили K ( t, λ). Для завершения расчетов нам нужно только найти b . Это число можно определить сравнением выражений

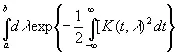(3.63)

и

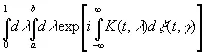. (3.64)

Таким образом, если при некоторых условиях, которые еще остается точно сформулировать, временной ряд допускает запись в виде (3.46) и известна функция ξ( t , γ) то мы можем определить функцию K ( t , λ) в (3.46) и числа а и b с точностью до неопределенной константы, прибавляемой к а , λ и b. Не возникает особых трудностей при b →+∞, также не слишком сложно распространить эти рассуждения на случай а → —∞. Конечно, предстоит проделать еще немалую работу, рассматривая задачу обращения функций в случае, когда результаты не однозначны, и общие условия справедливости соответствующих разложений. Тем не менее мы по крайней мере сделали первый шаг к решению задачи приведения обширного класса временных рядов к каноническому виду, что чрезвычайно важно для конкретного формального применения теорий предсказания и измерения информации, намеченных выше в этой главе.

Имеется, однако, одно очевидное ограничение, которое мы должны устранить из этого наброска теории временных рядов, а именно необходимость знать ξ( t , γ), и временной ряд, который мы разлагаем в виде (3.46). Вопрос ставится так: при каких условиях временной ряд с известными статистическими параметрами можно представить как ряд, определяемый броуновым движением, или по крайней мере как предел (в том или ином смысле) временных рядов, определяемых броуновым движением? Мы ограничимся временными рядами, [c.142]обладающими свойством метрической транзитивности и даже следующим более сильным свойством: если брать интервалы времени фиксированной длины, но отдаленные друг от друга, то распределения любых функционалов от отрезков временного ряда в этих интервалах приближаются к независимости по мере того, как интервалы отдаляются друг от друга [144]. Соответствующая теория уже излагалась автором.

Если K ( t ) — достаточно непрерывная функция, то можно показать, что нули величины

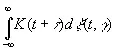(3.65)

по теореме М. Каца, почти всегда имеют определенную плотность и что эта плотность при подходящем выборе К может быть сделана сколь угодно большой. Пусть выбрано такое К D , что плотность равна D . Последовательность нулей величины

,

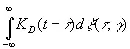от —∞ до ∞ обозначим через Z n ( D, γ), —∞< n <���∞. Конечно, при нумерации этих нулей индекс n определяется лишь с точностью до аддитивной целочисленной константы.

Пусть теперь T ( t, μ) — произвольный временной ряд от непрерывной переменной t , а μ — параметр распределения временных рядов, изменяющийся равномерно в интервале (0, 1). Пусть далее

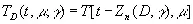, (3.66)

где Z n— нуль, непосредственно предшествующий моменту t . Можно показать, что, каково бы почти ни было μ, для любого конечного множества значений t 1, t 2, …, t v переменной х одновременное распределение величин T D ( t k , μ, γ) ( k =1, 2, …, v ) при D →∞ будет приближаться к одновременному распределению величин T ( t k, μ) для тех же t k при D →∞. Но T D ( t k , μ, γ) полностью определяется величинами t k , μ, D . Поэтому вполне уместно попытаться выразить T D ( t k , μ, γ) [c.143]для данного D и данного μ, либо прямо в виде (3.46), либо некоторым образом в виде временного ряда, распределение которого является пределом (в указанном свободном смысле) распределении этого типа.

Следует признать, что все это изображает скорее программу на будущее, чем уже выполненную работу. Тем не менее эта программа, по мнению автора, дает наилучшую основу для рационального, последовательного рассмотрения многих задач в области нелинейного предсказания, нелинейной фильтрации, оценки передачи информации в нелинейных системах и теории плотного газа и турбулентности. К ним принадлежат, быть может, самые острые задачи, стоящие перед техникой связи.

Перейдем теперь к задаче предсказания для временных рядов вида (3.34). Мы замечаем, что единственным независимым статистическим параметром такого временного ряда является функция Ф( t ), определенная формулой (3.35). Это значит, что единственной значащей величиной, связанной с K ( t ), является

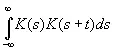(3.67)

Конечно, здесь К — величина действительная.

Применяя преобразование Фурье, положим

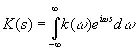. (3.68)

Если известно K ( s ), то известно k (ω), и обратно. Тогда

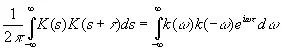(3.69)

Таким образом, знание Ф( t ) равносильно знанию k (ω) k (—ω). Но поскольку K(s) действительно, то

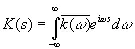, (3.70)

откуда 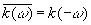. Следовательно, | k (ω)| 2есть известная функция, а потому действительная часть log| k (ω)| также есть известная функция. [c.144]

Если записать [145]

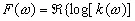(3.71)