Норберт Винер - Кибернетика или управление и связь в животном и машине

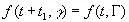, (3.36)

то преобразование параметра γ в Г сохраняет меру. Другими словами, наш временной ряд f ( t , γ) находится в статистическом равновесии.

Далее, если мы рассмотрим среднее значение для

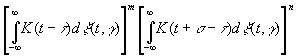(3.37)

то оно состоит в точности из членов выражения

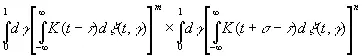(3.38)

[c.137]

и из конечного числа членов, имеющих множителями степени выражения

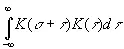, (3.39)

если последнее стремится к нулю при σ→∞, то (3.38) будет пределом выражения (3.37). Другими словами, распределения функций f ( t , γ) и f ( t +σ, γ) становятся асимптотически независимыми, когда σ→∞. Более общим, но совершенно аналогичным рассуждением можно показать, что одновременное распределение функций f ( t 1, γ), …, f ( t n , γ) и функций f (σ+ s 1, γ), …, f (σ+ s m , γ) стремится к совместному распределению первого и второго множества, когда σ→∞. Другими словами, если F [ f ( t , γ)] — любой ограниченный измеримый функционал, т. е. величина, зависящая от всего распределения значений функции f ( t , γ) от t , то для него должно выполняться условие

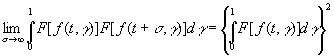. (3.40)

Если F [ f ( t , γ)] инвариантен при сдвиге по t и принимает только значения 0 или 1, то

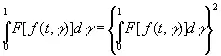, (3.41)

т. е. группа преобразований f ( t , γ) в f ( t +σ, γ) метрически транзитивна. Отсюда следует, что если F [ f ( t , γ)] — любой интегрируемый функционал от f как функции от t , то по эргодической теореме

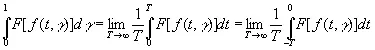(3.42)

[c.138]

для всех значений γ, исключая множество нулевой меры. Таким образом, мы почти всегда можем определить любой статистический параметр такого временного ряда (и даже любого счетного множества статистических параметров) из прошлой истории одного только параметра. В самом деле, если для такого временного ряда мы знаем

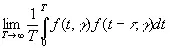(3.43)

то мы знаем Ф( t ) почти во всех случаях и располагаем полным статистическим знанием о временном ряде.

Некоторые величины, зависящие от временного ряда такого рода, обладают интересными свойствами. В частности, интересно знать среднее значение величины

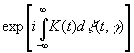(3.44)

Формально мы можем записать его в виде

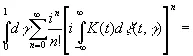
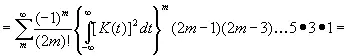
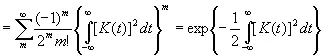. (3.45)

Весьма интересная задача — попытаться построить возможно более общий временной ряд из простых рядов броунова движения. При таких построениях, как подсказывает пример рядов Фурье, разложения типа (3.44) составляют удобные строительные блоки. В частности, исследуем временные ряды специального вида:

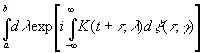(3.46)

[c.139]

Предположим, что нам известна функция ξ(τ, γ), а также выражение (3.46). Тогда при t 1> t 2находим, как в (3.45),

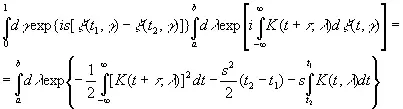(3.47)

Умножив на

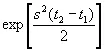
и положив s ( t 2— t 1)= i σ, получим при t 2→ t 1

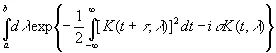(3.48)

Примем K ( t 1, λ) за новую независимую переменную μ и, решая относительно λ, получим

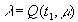(3.49)

Тогда выражение (3.48) будет иметь вид

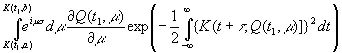(3.50)

Отсюда преобразованием Фурье можно найти

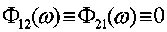(3.51)

как функцию от μ, коль скоро μ лежит между K ( t 1, a ) и K ( t 1, b ). Интегрируя эту функцию по μ, найдем

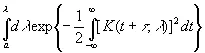(3.52)

[c.140]

как функцию от K ( t 1, λ) и t 1. Иначе говоря, существует известная функция F ( u, v ), такая, что

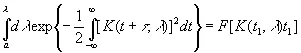(3.53)

Поскольку левая часть этого равенства не зависит от t 1, мы можем обозначить ее через G (λ) и положить

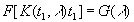(3.54)

Здесь F — известная функция, и ее можно обратить относительно первого аргумента, положив

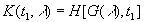, (3.55)

где H — также известная функция. Отсюда

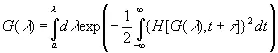(3.56)

Тогда выражение

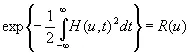(3.57)

будет известной функцией и

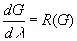(3.58)

откуда

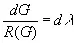, (3.59)

или

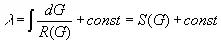. (3.60)