Норберт Винер - Кибернетика или управление и связь в животном и машине

Информация, поступающая обратно в управляющий центр, стремится противодействовать отклонению управляемой величины от управляющей, но она может зависеть от этого отклонения весьма различным образом. Простейшие управляющие системы — линейные системы: выходной сигнал исполнительного органа зависит линейно от входного сигнала, и при сложении входных сигналов складываются и выходные сигналы. Выходной сигнал отсчитывается каким-нибудь прибором, также линейным. Этот отсчет просто вычитается из входного сигнала. Мы хотим дать точную теорию работы такой системы и, в частности, исследовать ее неисправное поведение и возникновение в ней колебаний при неправильном обращении или перегрузке.

В этой книге мы по возможности избегали математической символики и математических методов, хотя в ряде мест, включая предыдущую главу, вынуждены были примириться с ними. Сейчас речь опять пойдет о вопросах, где математическая символика — самый надежный язык; избежать ее можно только ценой длинных перифраз, которые вряд ли будут понятны профану и которые поймет лишь читатель, знакомый с математической символикой, поскольку в его власти перевести их в символы. Наилучший компромисс, который мы можем выбрать, — это дополнять символику пространными словесными пояснениями.

Пусть f ( t ) — функция времени t , где t изменяется от —∞ до ∞; иначе говоря, f ( t ) — величина, принимающая определенное числовое значение для каждого момента t . В любой момент t нам доступны величины f ( s ), где s меньше или равно t , но отнюдь не больше t . [c.165]Мы располагаем устройствами, электрическими или механическими, которые задерживают входной сигнал на фиксированное время и выдают нам при входном сигнале f ( t ) выходной сигнал f ( t —τ), где τ — фиксированная задержка.

Мы можем включить одновременно несколько таких устройств, получив на выходах сигналы f ( t —τ 1), f ( t —τ 2),…, f ( t —τ n ). Каждый из этих выходных сигналов мы можем умножить на фиксированные величины, положительные или отрицательные. Так, при помощи потенциометра можно умножить напряжение на фиксированное положительное число, меньшее единицы, и не очень трудно изобрести автоматические компенсационные устройства и усилители, чтобы умножать напряжение на отрицательные величины или на величины, бо́льшие единицы. Нетрудно также составить простую электрическую схему для непрерывного сложения напряжений, при помощи которой мы получим выход

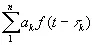. (4.01)

Увеличивая число задержек τ k и выбирая подходящим образом коэффициенты a k , мы можем сколь угодно приблизиться к выходному сигналу вида

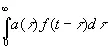. (4.02)

Обратим внимание на то существенное обстоятельство, что в этом выражении интегрирование производится от 0 до ∞, а не от —∞ до ∞. В противном случае мы могли бы с помощью различных практических устройств преобразовать наш сигнал в f ( t + σ ), где σ положительно. Но это предполагает знание будущего функции f ( t ), a f ( t ) может быть величиной, которая не определяется однозначно своим прошлым; пример — координаты трамвая, который может повернуть на стрелке в ту или другую сторону. Если физический процесс по видимости дает нам оператор, преобразующий f ( t ) в

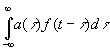(4.03)

[c.166]

где а (τ) не исчезает при отрицательных τ, это значит, что мы не имеем больше истинного оператора для f ( t ), определяемого однозначно прошлым этой функции. Такое может встретиться в реальных физических ситуациях. Например, динамическая система без входа может прийти в постоянные колебания или даже в колебания, нарастающие до бесконечности, с неопределенной амплитудой. В этом случае будущее системы не определяется ее прошлым, и мы, наверное, можем найти формализм, в котором бы использовался оператор, зависящий от будущего.

Операция, посредством которой получено выражение (4.02) из f ( t ), имеет еще два существенных свойства: 1) она не зависит от сдвига начального момента и 2) она линейна. Первое свойство выражается утверждением, что если

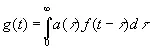, (4.04)

то

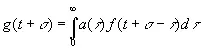. (4.05)

Второе выражается утверждением, что если

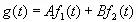, (4.06)

то

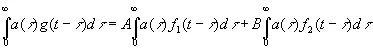. (4.07)

Можно показать, что в некотором подходящем смысле всякий оператор для прошлого функции f ( t ), линейный и инвариантный относительно сдвига начального момента, имеет вид (4.02) или является пределом последовательности операторов этого вида. Например, f’ ( t ) есть результат применения оператора с такими свойствами к f ( t ), и потому [c.167]

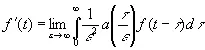, (4.08)

где

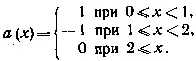(4.09)

Как мы уже видели, функции е zt составляют особенно интересное семейство с точки зрения оператора (4.02), поскольку

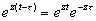, (4.10)

и оператор задержки становится просто множителем, зависящим от z . Оператор (4.02) переходит тогда в

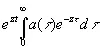. (4.11)

и также оказывается оператором умножения, зависящим только от z . Выражение

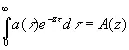(4.12)

называется представлением оператора (4.02) в виде функции частоты. Если z — комплексная величина х + iy , где х и y — действительные числа, то (4.12) переходит в

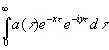(4.13)

Отсюда следует ввиду известного неравенства Шварца для интегралов, что если y >0 и