Норберт Винер - Кибернетика или управление и связь в животном и машине

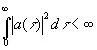, (4.14)

то [c.168]

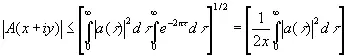. (4.15)

Это значит, что А ( х + iу ) — ограниченная голоморфная функция комплексной переменной в каждой полуплоскости x≥ε>0, а функция A ( iy ) представляет в некотором весьма определенном смысле граничные значения этой функции.

Положим

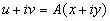, (4.16)

где u и v — действительные числа. Тогда x + iy определится как функция (не обязательно однозначная) от u + iv. Это функция аналитическая, хотя и мероморфная, за исключением точек u + iv , соответствующих точкам z=x + -iy , где ∂А ( z ) /∂z= 0. Граница х= 0 перейдет в кривую с параметрическим уравнением

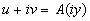( y действительное). (4.17)

Эта новая кривая может пересекать саму себя любое число раз, но в общем случае она будет делить плоскость на две области. Рассмотрим кривую (4.17), вычерченную в направлении возрастания y от —∞ до +∞. Если идти от нее вправо по непрерывной линии, не пересекающей снова кривую (4.17), можно попасть в те или иные точки плоскости. Точки, не входящие в это множество и не лежащие на кривой (4.17), мы будем называть внешними точками. Часть кривой (4.17), содержащую предельные точки внешних точек, назовем эффективной границей. Все остальные точки будут именоваться внутренними точками. На нашем чертеже с границами, проведенными в направлении стрелок (рис. 1), внутренние точки заштрихованы, а эффективная граница выделена жирной линией.

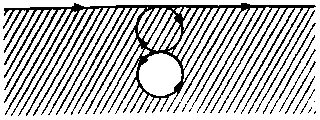
Рис. 1

[c.169]

Условие ограниченности функции А в любой правой полуплоскости указывает на то, что бесконечно удаленная точка не может быть внутренней точкой. Она может быть граничной точкой, хотя существуют весьма определенные ограничения на тип граничной точки, которой может быть бесконечно удаленная точка. Эти ограничения касаются «толщины» множества внутренних точек, простирающихся к бесконечности.

Мы переходим теперь к математической формулировке задачи о линейной обратной связи. Пусть структурная (не электрическая!) схема нашей системы имеет вид, как на рис. 2.

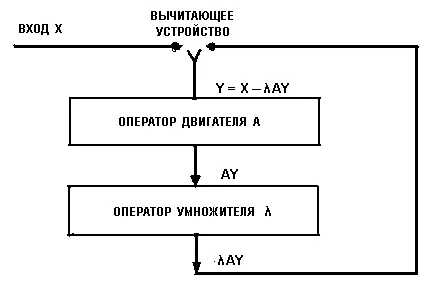
Рис. 2

Здесь входной сигнал двигателя, обозначенный через Y , равен разности между первоначальным входным сигналом Х и выходным сигналом умножителя, умножающего выходную мощность AY двигателя на коэффициент λ. Тогда

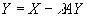(4.18)

и

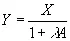, (4.19)

откуда выходной сигнал двигателя

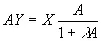. (4.20)

Следовательно, оператор, создаваемый всем механизмом обратной связи, равен A /(1+ λA ). Он будет бесконечно большим тогда и только тогда, когда А= —1 /λ. Кривая (4.17) для этого нового оператора будет иметь вид [c.170]

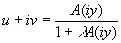, (4.21)

и ∞ будет внутренней точкой этой кривой тогда и только тогда, когда —1/ λ является внутренней точкой первоначальной кривой (4.17) [149].

В этом случае обратная связь с коэффициентом λ , несомненно, произведет нечто катастрофическое, и эта катастрофа практически выразится в том, что система придет в неограниченные, нарастающие колебания. Если же точка —1/ λ внешняя, то можно показать, что никаких неприятностей не будет, и обратная связь будет устойчивой. Случай, когда точка —1/ λ лежит на эффективной границе, требует особого исследования. В большинстве случаев система может прийти при этом в колебание с амплитудой, которая не будет увеличиваться.

Пожалуй, полезно рассмотреть несколько операторов А и допустимые для них диапазоны обратной связи. Мы будем рассматривать не только операции (4.02), но и их пределы, предполагая, что к последним применимы те же рассуждения.

Если оператор А соответствует дифференциальному оператору, то A ( z )= z ; тогда при изменении y от —∞ до ∞ точно так же изменяется и А ( y ), и внутренние точки являются внутренними точками правой полуплоскости. Точка —1/ λ всегда является внешней, и любая степень обратной связи возможна.

Если

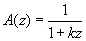, (4.22)

то кривая (4.17) принимает следующий вид:

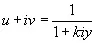, (4.23)

или

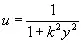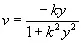, , (4.24)

что можно также записать в виде

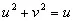(4.25)

[c.171]

Таким образом, наша кривая есть окружность с радиусом 1/2 и центром в точке (1/2, 0). Обход ее совершается по часовой стрелке, и внутренними будут те точки, которые обычно считаются внутренними. В этом случае обратная связь также неограниченна, ибо точка —1/λ всегда находится вне круга. Оператор a ( t ), соответствующий этому оператору А , будет равен

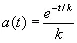. (4.26)

Положим теперь

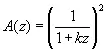, (4.27)

тогда (4.17) принимает вид

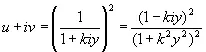(4.28)

Или

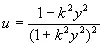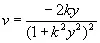, (4.29)