С. Виноградов - Логика. Учебник для средней школы. [Издание восьмое. Утверждён Министерством просвещения РСФСР.]

Средний термин может занимать в силлогизме различные положения: он может быть в обеих посылках подлежащим и сказуемым и может быть в одной посылке подлежащим, а в другой — сказуемым. В зависимости от положения среднего термина в посылках различают четыре фигуры силлогизма.

Эти фигуры можно изобразить следующими схемами:

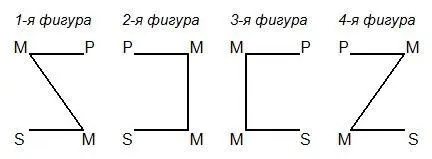
Каждая схема изображает две посылки и связь между посылками. Горизонтальные линии обозначают связь терминов в посылках, а наклонные и вертикальные линии — связь между посылками. Заключения на рисунке не показаны, так как их схема одинакова для всех фигур: S — P .

Симметричное положение терминов помогает легко запомнить различия фигур. Эти различия следующие:

1-я фигура . Средний термин является подлежащим большей посылки и сказуемым меньшей посылки.

Например:

Всякая религия ( М ) есть дурман для народа ( Р ).

Христианство ( S ) — религия ( М ).

---------------------------------------

Следовательно, христианство ( S ) есть дурман для народа ( Р ).

2-я фигура . Средний термин является сказуемым в обеих посылках — в большей и в меньшей.

Например:

Насекомые ( Р ) не имеют более трёх пар ног ( М ).

Пауки ( S ) имеют более трёх пар ног ( M ).

-------------------------------------

Следовательно, пауки ( S ) не насекомые ( Р ).

3-я фигура . Средний термин является подлежащим в обеих посылках — в большей и в меньшей.

Например:

Морские губки ( М ) не способны к самостоятельному передвижению ( Р ).

Морские губки ( М ) — животные ( S ).

----------------------------------------

Следовательно, некоторые животные ( S ) не способны к самостоятельному передвижению ( Р ).

4-я фигура редко употребляется в практике нашего мышления, и поэтому мы её здесь не рассматриваем.

В состав силлогизма входят суждения, разные по количеству и качеству: общеутвердительные, общеотрицательные, частноутвердительные и частноотрицательные. В зависимости от того или другого сочетания суждений получаются разновидности силлогизма, или модусы.

Например, силлогизм может состоять из трёх общеутвердительных суждений — это будет модус AAA .

Разумеется, не каждое сочетание трёх суждений может быть модусом. Например, невозможен модус ЕЕА (утвердительный вывод из отрицательных посылок), или IАО (отрицательный вывод из утвердительных посылок), или ЕОО (вывод из отрицательных посылок) и др.

Модусами являются такие сочетания суждений, которые не противоречат правилам категорического силлогизма.

Примеры:

1-я фигура . А . Всякое движение ( М ) есть движение материи ( Р ).

Модус AAA . А . Перемещение тела в пространстве ( S ) есть движение ( М ).

------------------------------------

А . Перемещение тела в пространстве ( S ) есть движение материи ( Р ).

2-я фигура . Е . Ни один сторонник мира и демократии ( Р ) не поддерживает агрессоров ( М ).

Модус ЕАЕ . А . Правые социалисты ( S ) поддерживают агрессоров ( М ).

------------------------------------

Е . Правые социалисты ( S ) не являются сторонниками мира и демократии ( Р ).

3-я фигура . А . Росянка ( M ) питается насекомыми ( Р ).

Модус ААI . А . Росянка ( М ) — растение ( S ).

------------------------------------

I . Некоторые растения ( S ) питаются насекомыми ( Р ).

Состав модусов каждой фигуры определяет её особые правила, а именно:

1-я фигура . Большая посылка должна быть обязательно общей, а меньшая — утвердительной.

Возьмём такое умозаключение, где меньшая посылка отрицательная:

А . Во всех городах за полярным кругом бывают белые ночи.

Е . Ленинград не находится за полярным кругом.

-----------------------------------

Е . В Ленинграде не бывает белых ночей.

Но в Ленинграде бывают белые ночи. Вывод в нашем примере получился неправильный, так как оказалось нарушенным правило первой фигуры (ср. третье правило силлогизма).

2-я фигура . Большая посылка должна быть обязательно общей, а одна из посылок — отрицательной.

Из этого следует, что заключение по 2-й фигуре всегда отрицательное.

Согласно этому правилу, невозможно было бы такое умозаключение:

Все металлы проводят электричество.

Данное вещество проводит электричество.

--------------------------------

Данное вещество — металл.

Такой силлогизм был бы неверным, так как в нём нарушено правило второй фигуры (ср. второе правило силлогизма).

3-я фигура . Меньшая посылка должна быть обязательно утвердительной, а заключение — частным.

Таковы правила фигур силлогизма. Эти правила фигур являются применением к фигурам общих правил силлогизма.

Фигуры и модусы силлогизма правильны постольку, поскольку они отражают реально существующие отношения вещей. Всякое отклонение от правильных форм именно потому и становится неправильным, что оно не отражает действительности.

Отсюда вытекает познавательное значение силлогизма как формы мышления: правильные модусы силлогизма, являясь отражением реально существующих отношений, дают нам возможность познать эти реальные отношения.

Возьмём, например, модус AЕЕ . Он отражает простой факт действительности: если все предметы данного класса обладают каким-то определённым признаком, а интересующий нас предмет этим признаком не обладает, то, значит, интересующий нас предмет не входит в число предметов данного класса.

Например: если всякая живая клетка содержит в себе белок, а кристаллы гипса не содержат белка, то, следовательно, они не входят в число живых клеток.

Это простое отношение вещей запечатлелось в нашем сознании в форме модуса AЕЕ . Но такое же происхождение имеют и все другие модусы силлогизма, которые также отражают те или другие отношения вещей.

Это и даёт нам возможность в форме того или другого модуса силлогизма познавать действительность.

Так, модусами первой фигуры мы пользуемся в тех случаях, когда нам надо единичный или частный случай подвести под общее положение или же из более общего вывести менее общее.

Например, мы знаем природу и свойства гремучего газа, и если во время опытов с водородом в пробирке получился взрыв, то мы этот частный случай подводим под наше общее знание о смесях водорода и делаем заключение: взорвался гремучий газ.