Лиза Рэндалл - Закрученные пассажи: Проникая в тайны скрытых размерностей пространства.

Ниже мы рассмотрим интересный подход, в котором пятимерное пространство-время искривлено. Но для начала сосредоточимся на двух бранах на краях пятого измерения. Эти две граничные браны совершенно плоские. Находясь на бране на любой из границ, вы будете прикреплены к (три + один) — мерному миру (три пространственных измерения и одно временное) [154] Я иногда буду использовать запись «три + один» вместо «четыре», чтобы подчеркнуть различие между пространством и временем. , который будет простираться бесконечно далеко по трем пространственным измерениям и выглядеть как плоское пространство-время, без особых гравитационных эффектов.

Кроме того, искривленное пространство-время обладает тем специальным свойством, что если вы ограничитесь любым отдельным срезом вдоль пятого измерения, но не самими бранами на краях, вы обнаружите, что этот срез совершенно плоский. То есть, хотя нигде в пятом измерении за исключением концов нет бран, геометрия (три + один) — мерных поверхностей, которые вы получаете, находясь в какой-либо пятимерной точке, выглядит плоской, т. е. имеет ту же форму, что и большие плоские браны на границах. Если вы рассматриваете граничные браны как горбушки у буханки хлеба, то плоские параллельные четырехмерные области в любой точке вдоль пятого измерения пространства-времени похожи на плоские, нарезанные куски хлеба из внутренней части буханки.

Но тем не менее рассматриваемое нами пятимерное пространство искривлено. Это отражается в том способе, которым четырехмерные плоские срезы пространства-времени склеены вместе вдоль пятого измерения. Впервые я говорила об этой геометрии в институте теоретической физики Кавли в Санта-Барбаре, где теоретик-струнник Том Бэнкс объяснил мне, что с технической точки зрения пятимерная геометрия, которую нашли Раман и я, называется закрученной. Хотя многие искривленные геометрии пространства-времени в разговорной речи называются закрученными, технический термин относится к геометриям, в которых каждый срез плоский [155] На самом деле все срезы обладают одной геометрией; в данном случае срезы плоские. , но они собираются вместе с учетом общего закручивающего конформного фактора. Этот фактор есть функция, меняющая общий масштаб для положения, времени, массы и энергии в каждой точке в пятом измерении. Такое замечательное свойство закрученной геометрии достаточно тонкое, и я объясню его позднее в следующем разделе. Конформный фактор сказывается также на функции вероятности гравитона и взаимодействиях, которые мы вскоре изучим.

Искривленное пространство с плоскими слоями изображено на рис. 79. Это заполненная воронка. Мы могли бы с помощью большого ножа нарезать воронку на плоские листки, но поверхность воронки явно искривлена. В некоторых отношениях это похоже на искривленное пространство-время, которое мы рассматриваем. Но аналогия не идеальна, так как граница воронки, ее поверхность есть единственное место, где она искривлена, в то время как в закрученном пространстве-времени кривизна есть везде. Эта кривизна отражалась бы в общем изменении масштаба измерительной линейки в пространстве и скорости хода часов для времени, которые будут разными в каждой точке пятого измерения.

Более простой способ проиллюстрировать кривизну закрученного пространства-времени — обратиться к форме функции вероятности гравитона. Гравитон — это частица, переносящая гравитационное взаимодействие, и его функция вероятности говорит нам о вероятности обнаружения гравитона в любой фиксированной точке пространства. Интенсивность гравитации отражается в этой функции: чем больше ее значение, тем сильнее взаимодействия гравитона в этой конкретной точке и тем сильнее сила тяготения.

Для плоского пространства-времени гравитон будет с равной вероятностью обнаруживаться везде. Функция вероятности для гравитона в плоском пространстве-времени была бы поэтому постоянной. Но для искривленного пространства-времени, как и для закрученной геометрии, которую мы рассматриваем, это уже будет не так. Кривизна говорит нам о форме гравитации. Когда пространство-время искривлено, значение функции вероятности гравитона различно в разных местах пространства-времени.

Так как каждый срез пространства-времени в нашей закрученной геометрии совершенно плоский, функция вероятности гравитона не изменяется вдоль трех стандартных пространственных измерений, а меняется только вдоль пятого измерения [156] Напомним, что пятое измерение — это пятое измерение пространства-времени и гипотетическое четвертое измерение пространства. . Иными словами, даже несмотря на то, что функция вероятности гравитона имеет разные значения в разных местах вдоль пятого измерения, до тех пор пока две точки равноудалены вдоль пятого измерения, значение этой функции будет одним и тем же. Это говорит нам, что функция вероятности гравитона зависит только от положения в пятом измерении. Тем не менее она полностью характеризует кривизну закрученного пространства-времени. И так как эта функция изменяется только вдоль одной координаты, т. е. вдоль пятого измерения, ее просто изобразить на рисунке.

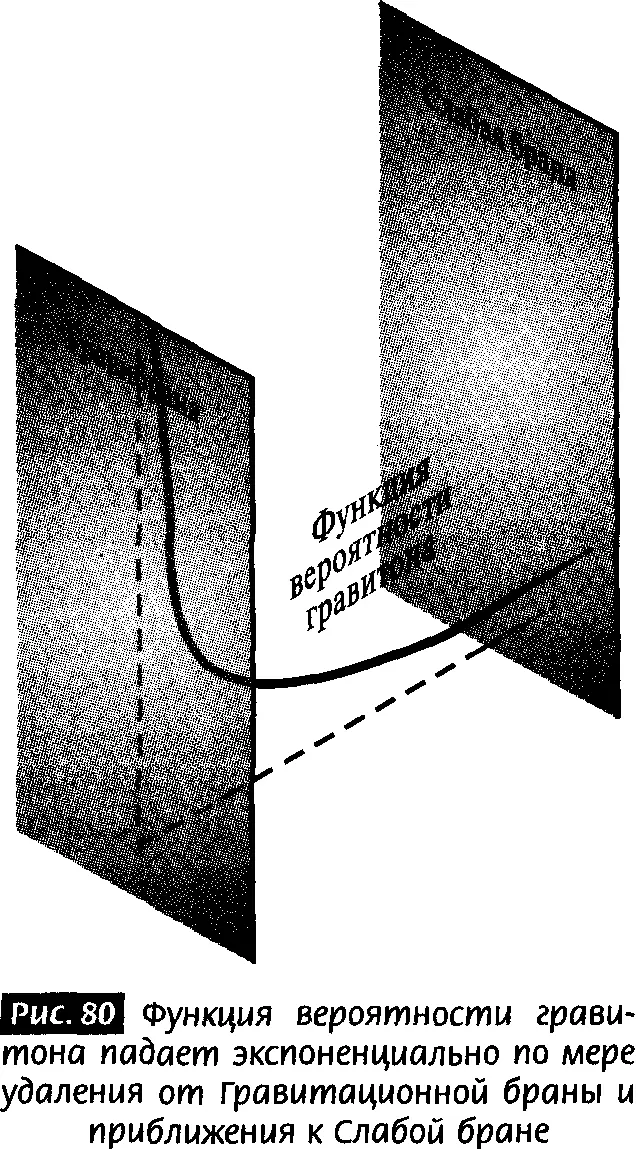
Функция вероятности гравитона вдоль пятого измерения изображена на рис. 80. Она экспоненциально быстро (т. е. необычайно быстро) убывает, как только мы покидаем первую брану, которую мы назовем Гравитационной браной, и направляется в сторону второй браны, которую мы назовем Слабой браной. Гравитационная брана и Слабая брана различны, так как первая несет положительную энергию, а вторая несет отрицательную энергию. Такое распределение энергии приводит к тому, что функция распределения гравитона намного больше в окрестности Гравитационной браны.

Эффект падения функции вероятности состоит в том, что гравитон, физическая частица, обмен которой генерирует гравитационное притяжение, имеет очень мало шансов быть найденным вблизи Слабой браны. Поэтому взаимодействия гравитона на Слабой бране сильно подавлены.

Интенсивность гравитации так сильно зависит от положения в пятом измерении, что интенсивности гравитационного взаимодействия на двух бранах, ограничивающих противоположные концы такого закрученного пятимерного мира, очень сильно различаются. Гравитация сильна на первой бране, где гравитация локализована, но очень слаба на второй бране, где находится Стандартная модель. Так как функция вероятности гравитона пренебрежимо мала на второй бране, взаимодействия гравитона с захваченными здесь частицами Стандартной модели оказываются чрезвычайно слабыми.