С. Капица - Синергетика и прогнозы будущего

Обсуждаемая модель отражает еще одну коллизию науки конца века. Триумфом химии стало открытие универсальных кирпичиков – элементов, из которых построена Вселенная; физика элементарных частиц тоже преуспела в изучении первооснов вещества, – этот список успехов анализа, выделения простейшего, можно продолжить. Но почему этих кирпичиков столько, а не больше? И каковы законы синтеза, объединения. Почему в малые работоспособные группы объединяются так, а не иначе? Почему не возникает далеких стабильных трансурановых элементов? Каким законам природы это противоречит? Почему в развитых странах не возникает одной "сверхмонополии", полностью контролирующей, к примеру, всю автомобильную промышленность или компьютерную индустрию? Эти вопросы, впрямую связанные с проблемой организации процессов, людей, структур, являются трудными для современной научной парадигмы. Их XX в. оставляет в наследство своему преемнику. И в этой связи, каждый случай, где в законах организации удается разобраться в деталях, представляется весьма ценным. Таким случаем и является обсуждаемая модель.

В этой модели есть еще один парадоксальный режим. Допустим, что нелинейность очень велика ( 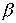> 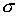+3), работы в рассматриваемом научном направлении очень перспективны. При этом процессы могут идти в виде волны падающей амплитуды (см. рис.20) (HS-режим без обострения). От конкретных результатов сначала проблема переходит на уровень "научного фольклора", а потом складывается ситуация, когда идеи "витают в воздухе" и никак не найдут, куда приземлиться. Но эта ситуация неустойчива, – небольшая группа энтузиастов, небольшой "студенческий проект" и ситуация радикально меняется, возникает быстрый процесс (реализуется LS-режим с обострением). Наверное, каждый может припомнить десяток ситуаций, когда классик в науке сделал то, что "все предвидели", про что "где-то слыхали", но до чего просто "руки никак не доходили".

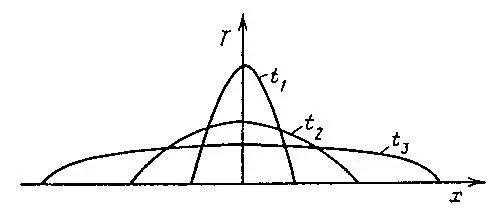
Рис. 20. HS-режим без обострения, возможный, когда 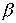> 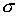+3. Решение существует бесконечно долго, амплитуда распространяющейся волны уменьшается. vspace-3mm endfigure

С обсуждаемой моделью связано много странных и удивительных вещей. С ней связано начало нескольких изящных математических теорий, любопытные физические эффекты, возможности создания оригинальных технологий. Она как бы притягивает новых исследователей, являясь полигоном и пробным камнем для новых подходов. Приведем только один пример такого сорта.

Часто задают следующий "неуместный" вопрос:"Почему следует всерьез относиться к решениям одной, пусть даже очень красивой задачи, в которой нелинейные зависимости имеют совершенно конкретный вид? Ведь степенные функции – это капля в океане всех возможных нелинейностей". И это действительно так. Более того, этот вопрос является очень общим. Огромное количество фундаментальных законов определяются степенными нелинейностями. Закон всемирного тяготения, закон Кулона и прочие, прочие, прочие. Если бы притяжение зависело от расстояния не по закону обратных квадратов, то орбиты планет Солнечной системы, к примеру, были бы незамкнуты (впрочем, здесь есть еще один выделенный степенной показатель). Исследователи так называемого антропного принципа установили, что для того, чтобы во Вселенной мог появиться человек, мировые константы должны были быть подогнаны очень точно. Но степенные зависимости в фундаментальных законах природы представляются еще более важными. Почему же нашему миру так повезло? В общем случае на этот вопрос нет хорошего ответа.

Однако в частном случае обсуждаемой модели он есть! Представим себе, что нелинейные функции k(T) и Q(T) нелинейны и решение растет в режиме с обострением. Математическая теория, принципиальный вклад в создание которой внес В.А.Галактионов, показывает, что при стремлении к моменту обострения задача вырождается. Ее решение начинает вести себя либо как решение уравнения с экспоненциальными источниками, либо как некоторое уравнение типа Гамильтона-Якоби (уравнения такого типа обычно возникают в классической механике). Либо как исходная задача со степенными источниками! И только в последнем случае есть сложные структуры. Ситуация здесь оказывается похожа на головоломку, которая имеет парадоксальное, но единственное решение.

Ну вот, наверное, и все об этой модели – одном из "кубиков", который есть в "конструкторе" нелинейной динамики. В одних случаях (как при описании роста народонаселения, он применим непосредственно), в других (как при моделировании ряда исторических процессов или при описании систем расселения) он указывает направление движения, в третьих выступает как интригующая метафора.

В конце этой главы сформулируем и обсудим вопрос, который не раз возникал у авторов этой книги и, вероятно, у многих специалистов по нелинейной науке. Почему взгляды и представления, выработанные при исследовании весьма узкого класса математических моделей небольшого круга явлений, выдвигаемые несколькими научными школами, оказывают возрастающее влияние на современную науку и на другие области культуры? Почему результаты анализа систем реакция-диффузия, простейших отображений философы воспринимают как оригинальную метафору, физики – как стимул для поиска новых явлений, математики – как постановки новых проблем в своей области? Живой отклик биологов, астрофизиков, экологов, политологов, представителей многих других дисциплин убеждает, что это не случайность.

Подчеркнем парадоксальность этой ситуации. Неклассическая наука, связанная с созданием теории относительности и квантовой механики, очень быстро и глубоко изменила мировоззрение. Вместе с тем обе теории дают адекватное объяснение, которое не может быть получено в классических рамках, для весьма экзотической части реальности. С движением при околосветовых скоростях, измерениями на микромасштабах, не говоря уже об излюбленном объекте специалистов по общей теории относительности – черных дырах, с которыми мы в повседневной жизни встречаемся далеко не каждый день. Да и физикам приходится прилагать немалые усилия, чтобы экспериментально изучать такие объекты.

Вместе с тем философы и естественники, занявшиеся осмыслением результатов неклассической науки, оказались правы. Знание таких деталей мироздания дало новые возможности, оказалось огромной силой. Атомные бомбы и лазеры открывают огромный список воплощений этого знания.