Шинтан Яу - Теория струн и скрытые измерения Вселенной

Помимо общефилософских выводов, следующих из доказательства гипотезы о положительности массы, эта — теперь уже — теорема дает некоторые подсказки по поводу природы массы как таковой, представляющей собой весьма эфемерное и на удивление неуловимое понятие в общей теории относительности. Частично эти сложности проистекают из нелинейности самой теории. Эта нелинейность означает то, что гравитация также является нелинейной. Благодаря этому гравитация может взаимодействовать сама с собой и в процессе взаимодействия порождать массу — тот ее вид, с которым особенно сложно иметь дело.

В общей теории относительности масса может быть определена только как глобальное понятие. Иными словами, мы привыкли оперировать понятием массы системы как целого, представляя эту систему заключенной в гипотетический ящик, так, как если бы мы посмотрели на нее из очень сильно удаленной точки — по сути, из бесконечности. Что касается «локальной» массы — например, массы данного тела, — то, хотя это понятие и покажется проще для непрофессионала в нашей области, на сегодняшний день четкого определения оно не имеет. Понятие плотности в общей теории относительности также определено весьма нечетко. Вопрос о том, откуда берется масса и как дать ей определение, волновал меня на протяжении десятилетий и, когда позволяло время, я возвращался к нему совместно с коллегами, такими как Мелисса Лю и Мутао Ванг из Колумбии. Как мне сейчас кажется, нам удалось в конце концов конкретизировать понятие локальной массы, используя при этом идеи различных физиков и геометров, и, возможно даже, мы были недалеки от окончательного решения проблемы. Но мы не смогли бы даже начать думать над этой проблемой, если бы не имели в основе прочного фундамента в виде положительности общей массы.

К тому же гипотеза о положительности массы привела нас с Шоном к доказательству другого утверждения из области общей теории относительности, касающегося так называемых черных дыр. Большинство людей, размышляя о столь причудливых астрофизических объектах, как черные дыры, едва ли как-то связывают их с геометрическими понятиями. Тем не менее геометрия достаточно многое может сказать о черных дырах, и по сути именно ей мы обязаны самой возможностью предсказания существования таких объектов до их обнаружения астрономическими методами. Это предсказание стало триумфом применения геометрического подхода к общей теории относительности.

В 1960-х годах Стивен Хокинг и Роджер Пенроуз при помощи геометрических методов, точнее, той особой разновидности геометрии, которая рассматривается в нашей книге, и законов общей теории относительности доказали, что любая ловушечная поверхность , то есть чрезвычайно искривленная поверхность, которую не может покинуть даже свет, обязана в конце концов эволюционировать в сингулярность того типа, который, как полагают, находится в центре черной дыры — в том месте, где кривизна пространства-времени стремится к бесконечности. Оказавшись в черной дыре, можно обнаружить, что при движении к центру кривизна будет неуклонно возрастать. Предела этому возрастанию попросту не существует — кривизна будет возрастать вплоть до самого центра, где ее величина станет равной бесконечности. С кривизной вообще связано много удивительных вещей. Прогуливаясь по поверхности Земли, имеющей огромный (порядка шести тысяч километров), по сравнению с нашим ростом (как правило, не большим двух метров), радиус, мы не ощущаем ее кривизны. Однако если бы мы решили совершить прогулку по планете с радиусом 5-10 метров, такой как планета Маленького Принца у Антуана де Сент-Экзюпери, то пренебречь ее кривизной мы бы уже не смогли.

Рис. 3.10а.Стивен Хокинг, физик из Кембриджского университета (фотография Филиппа Уотерсона, LBIPP, LRPS)

Рис. 3.10б.Роджер Пенроуз, математик из Оксфордского университета (© Роберт С. Харрис [Лондон])

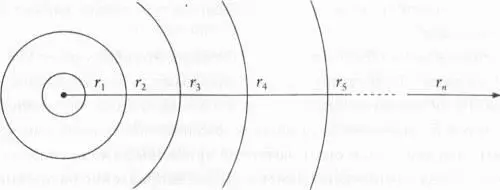
Рис. 3.11.Чем меньше сфера, тем сильнее она искривлена. Напротив, при стремлении радиуса к бесконечности кривизна уменьшается до нуля

Поскольку кривизна сферы обратно пропорциональна квадрату радиуса, возрастание радиуса до бесконечности приводит к уменьшению кривизны до нуля. И напротив, при стремлении радиуса к нулю кривизна неуклонно возрастает и стремится к бесконечности.

Представим себе вспышку света, произошедшую одновременно во всех точках поверхности обычной двухмерной сферы в трехмерном пространстве. Свет будет двигаться вдоль радиуса в двух направлениях — внутрь и наружу. Для лучей света, направленных к центру сферы, совокупность точек, до которых доходит свет в определенный момент времени, будет представлять собой поверхность, площадь которой быстро уменьшается и в пределе стремится к нулю, тогда как площадь подобной поверхности для лучей, распространяющихся вовне, со временем будет неуклонно возрастать. Ловушечная поверхность отличается от обычной сферы тем, что описанная выше площадь уменьшается вне зависимости от направления движения. [33] Roger Penrose, “Gravitational Collapse: The Role of General Relativity,” 1969, reprinted in Mathematical Intelligencer 30 (2008): 27–36. Какое направление ни выберешь — из ловушки не выбраться. Иными словами, пути наружу в данном случае нет.

Как такое может быть возможно? Отчасти это обусловлено тем, что ловушечная поверхность по определению должна обладать такими свойствами. Но объяснение также кроется и в том, что для ловушечных поверхностей так называемая средняя положительная кривизна имеет экстремум. Под действием столь заметной кривизны даже идущие наружу лучи света будут вынуждены изменить свое направление на противоположное, как если бы крыша и стены начали надвигаться на них, и в результате сойтись в центре. «Если площадь поверхности изначально уменьшается, то она будет продолжать уменьшаться, поскольку здесь работает эффект фокусировки, — объяснил это явление мой коллега Шон. — Можно представить себе расходящиеся круги на глобусе с центром на Северном полюсе, которые, благодаря положительности кривизны сферы, сходятся в точку на Южном полюсе. Подобный эффект фокусировки дает положительная кривизна». [34] Richard Schoen (Stanford University), interview with author, January 31, 2008.

Пенроуз и Хокинг доказали, что, однажды возникнув, ловушечные поверхности обязательно вырождаются в объекты, которые свет не может покинуть, — так называемые черные дыры. Но как возникают ловушечные поверхности? До того как мы с Шоном начали свою работу над этим вопросом, было принято считать, что единственным условием для формирования черной дыры является достаточно высокая плотность материи в некоторой области пространства, — впрочем, аргументы были весьма расплывчаты и показывали скорее нежелание вникать в суть проблемы. Никому до нас не удавалось сформулировать утверждение о природе ловушечных поверхностей в ясном и строгом виде. Именно эту проблему мы с Шоном избрали своей целью, и снова в дело пошел метод минимальных поверхностей, столь детально разработанный нами во время доказательства теоремы о положительности массы.