Шинтан Яу - Теория струн и скрытые измерения Вселенной

Рис. 5.1.Математик Ш. Ю. Ченг (фотография Джорджа М. Бергмана)

Метод непрерывности был назван так потому, что он подразумевает непрерывное преобразование решения некоего известного уравнения вплоть до его полного совпадения с решением искомого. Процедуру преобразования, как правило, разбивают на две части, одна из которых работает только в непосредственной близости от известного решения.

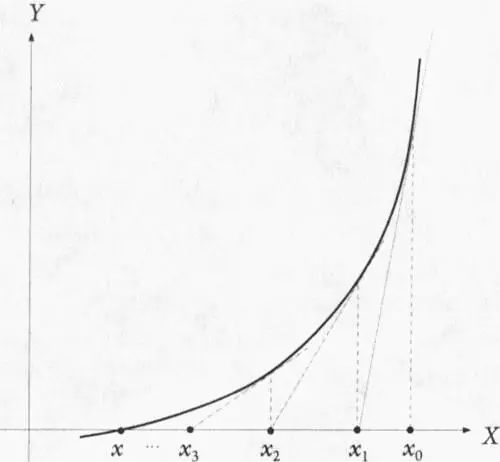
Рис. 5.2.Наглядная иллюстрация метода Ньютона. Для того чтобы найти точку пересечения определенной кривой или функции с осью X , сначала нужно наугад подобрать некую точку x 0 наиболее подходящую для этого. Затем необходимо провести касательную к кривой в точке x 0 и отметить точку, в которой эта касательная пересечет ось X (это будет точка x 1 ). В том случае, если наше изначальное предположение не было полностью ошибочным, продолжая этот процесс, мы будем получать точки все ближе и ближе к искомой

Одна из этих частей носит название метода Ньютона, так как она в определенной степени основана на методе, разработанном Исааком Ньютоном более трехсот лет назад. Для того чтобы продемонстрировать этот метод в действии, рассмотрим функцию y=x 3-3x+1 , которая описывает кривую, пересекающую ось X в трех различных точках, являющихся корнями этого полинома. Подход, предложенный Ньютоном, позволяет определить положение корней на оси X , что далеко не всегда можно сделать, просто взглянув на уравнение. Предположим, что напрямую решить уравнение нельзя, однако один из корней соответствующей функции можно найти вблизи точки x 1. Касательная, проведенная к кривой в этой точке, пересечет ось X в другой точке — x 2 , находящейся ближе к искомому корню, чем точка x 1 . Если мы проведем касательную в точке x 2 , она пересечет ось X в точке x 3 , которая будет еще ближе к искомому корню. Таким образом, многократное повторение данной процедуры должно довольно быстро привести нас к искомому корню, если только начальная точка x 1 была выбрана более-менее удачно.

В качестве еще одного примера рассмотрим набор уравнений E t только одно из которых, Е 0 (для которого t = 0 ), мы способны решить. При этом в действительности нам нужно решить уравнение E 1 (для которого t = 1 ). Мы могли бы использовать метод Ньютона, если мы находимся в непосредственной близости к точке t = 0 , решение уравнения в которой хорошо известно, но этот подход не может привести нас к 1 . В этом случае необходимо прибегнуть к другому методу оценки, обладающему большей применимостью.

Как же это сделать? Представим, что над Тихим океаном была запущена ракета, которая приземлилась в радиусе ста миль от атолла Бикини. Это дает нам некоторое представление о том, где ракета может быть, другими словами — ее общую позицию, но мы хотели бы знать больше, например ее скорость, или ее ускорение, или как это ускорение изменялось в течение полета. Это можно сделать при помощи дифференциального исчисления — путем взятия первой, второй и третьей производных от функции, описывающей зависимость положения ракеты от времени. С таким же успехом можно брать производные и более высоких порядков, но для эллиптических уравнений второго порядка того типа, которым я занимаюсь, третьей производной вполне хватает.

Одного лишь знания производных функции недостаточно, хотя задача по их нахождению сама по себе может быть чрезвычайно трудоемкой. Кроме того, производные нужно «контролировать». Иными словами, необходимо установить для них границы — удостовериться, что они не могут быть ни чрезвычайно велики, ни чрезвычайно малы. Только в этом случае полученные решения будут «стабильны» — то есть не будут бесконтрольно раздуваться, тем самым дисквалифицируя себя как решения и разрушая наши надежды на них. Итак, взяв для начала нулевую производную — то есть исходную функцию, описывающую изменение положения ракеты с течением времени, мы устанавливаем для нее наличие верхних и нижних границ — иными словами, делаем оценки, показывающие, что решение по крайней мере возможно. Та же самая операция проводится для всех производных более высоких порядков, что позволяет удостовериться в том, что они не являются ни бесконечно большими, ни бесконечно малыми, а функции, их описывающие, не флуктуируют совершенно беспорядочным образом. Это позволяет априори оценить скорость, ускорение, зависимость ускорения от времени и т. д. Если мы можем таким образом проверить все производные от нулевой до третьей, значит, у нас есть хороший способ оценить уравнение в целом и приличный шанс найти его решение. Подобный процесс оценки и доказательства того, что оценочные данные сами по себе находятся под контролем, как правило, представляют самую сложную часть всего процесса.

Итак, в конце концов, все сводится к оценкам. Есть что-то ироническое в моем признании их актуальности для решения проблемы, с которой я столкнулся. Помню, когда я впервые попал в Беркли, в коридоре математического факультета я столкнулся с двумя постдоками из Италии. Они прыгали с радостными криками. На мой вопрос о том, что произошло, они ответили, что им только что удалось получить приближенную оценку. Когда же я спросил их о том, что это такое — оценка, они посмотрели на меня как на полного невежду, непонятно как попавшего в это здание. Именно с этого момента я пытался узнать как можно больше об априорных оценках. Калаби получил такой же урок несколькими десятилетиями ранее от своего друга и соратника Луиса Ниренберга: «Повторяй за мной, — говорил тогда Ниренберг, — без априорных оценок ты никогда не сможешь решать дифференциальные уравнения в частных производных!» [50] Calabi, interview, May 14, 2008. А в начале 1950-х Калаби переписывался с Эндрю Вейлем по поводу своей гипотезы. Вейль, который полагал, что математические технологии того времени просто не созрели для нахождения решения, спрашивал Калаби: «Как вы собираетесь получить оценки?» [51] Eugenio Calabi, interview with author, June 16, 2008.

Два десятилетия спустя, когда я включился в игру, сама проблема не изменилась. Она по-прежнему оставалась невероятно сложной, хотя математический аппарат за это время успел развиться настолько, что решение стало в принципе возможным. Проблема состояла лишь в том, чтобы найти верный подход или, по крайней мере, создать необходимую точку опоры. Так что я подобрал более простое уравнение, а затем постарался показать, что его решение может в конечном счете «деформироваться» в решение более сложного уравнения.