Г. Басина - Синергетика. Основы методологии

То же самое можно сформулировать и по-другому. Соотношения вероятностей попадания системы в одно из возможных состояний до и после события резко изменились. До события система еще имела возможность попасть в любое из допустимых состояний. После события возможность попадания во все состояния, кроме одного, оказались равными нулю.

Наблюдатель системы приобрёл значительную новую информацию не только о настоящем, но и о будущем системы. Здесь, как и ранее для случая с двумя исходами интуитивно появляется понятие информации как результата отождествления системы, которая до свершения события могла с некоторой вероятностью оказаться в одном из возможных состояний с некоторым конкретным состоянием.

Нашему рассмотрению может быть дана и другая математическая интерпретация. Пусть мы имеем фазовое пространство взаимодействующих структур, имеющее n аттракторов — зон притяжения; существует некоторая точка (или область), отделяющая друг от друга бассейны притяжения этих аттракторов. Перед событием фазовое состояние системы взаимодействующих структур попадает в указанную точку или область, выйдя из которой в процессе события оно попадает в бассейн притяжения того или иного аттрактора, откуда ей уже не вернуться назад.

В классической теории вероятностей вместо вектора/) вводится некоторая функция на множестве возможных исходов бифуркационного (случайного) события.

Рассматривается в элементарном случае конечное множество Ω элементов ω, которые мы будем называть элементарными исходами бифуркационного события и ξ(Ω) множество подмножеств из Ω. Элементы множества φ(Ω) будем называть совокупностями исходов бифуркационного события, а Ω — пространством элементарных исходов бифуркационного события.

Каждому элементу ω из Ω поставлено в соответствие неотрицательное действительное число p 1, — вероятность реализации i-го исхода бифуркационного события. При этом выполняется условие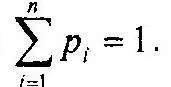

В этом случае p 1, …, p nсуть вероятности элементарных исходов ω 1, …, ω nили просто элементарные вероятности.

Каждому множеству A из ξ(Ω) поставлено в соответствие неотрицательное действительное число P(A). Это число называется вероятностью реализации совокупности исходов. Оно определяется как сумма вероятностей элементарных исходов, входящих в A:

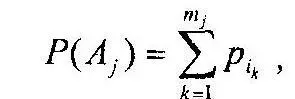
где i k— номера элементарных исходов, входящих в совокупность A j.

Если P(A) > 0, то частное Р(В\А) = Р(АВ)/Р(А), где AB — пересечение множеств А и В, называется условной вероятностью реализации совокупности исходов В при условии реализации совокупности исходов. Отсюда непосредственно следует, что Р(АВ) = Р(В\А)Р(А).

Заключение по индукции даёт общую формулу Р(А 1А 2…А n) = Р(А 1)Р(А 2\А 1)P(A 3\A 2\A 1)…Р(А n\А 1…А n-1) (теорема умножения).

Отсюда получаем Р(А\B) = Р(А)Р(В\А)/Р(B), и далее формулу полной вероятности Р(В) = P(A 1)P(B\A 1) + P(A 2)P(B\A 2) +…+ P(А n)P(B\А n),

где А 1+А 2+…+ А n= Ω и В — произвольная совокупность исходов, и формулу Байеса:

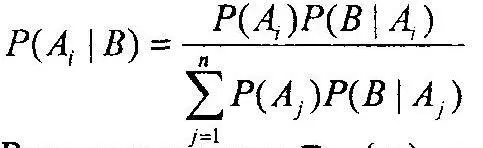
Введение вектора α = {α 1}, где α i=Υр i, позволяет вместо некоторой аддитивной меры, рассматривать метрический вектор единичной длины в евклидовом пространстве. В этом случае вся изложенная выше теория может быть переформулирована в терминах амплитуды вероятности.

Каждому множеству А из ξ(Ω) может быть поставлено в соответствие неотрицательное действительное число Аp(А). Это число называется амплитудой вероятности реализации совокупности исходов А. Оно определяется как корень квадратный из суммы квадратов амплитуд вероятности элементарных исходов, входящих в А:

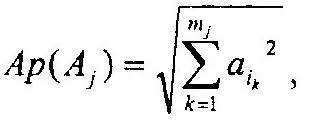
где i k— номера элементарных исходов, входящих в совокупность А j. Ар(Ω) = 1. Если А и B не пересекаются, то [Ap(A+B)] 2=[Ар(А)] 2+ [Ар(В)] 2.

Каждому множеству А j, состоящему из m jэлементарных исходов бифуркационного события, соответствует некоторый m j-мерный евклидов вектор Ар(А j) = {a jk} k = 1,…,m j, модуль которого равняется

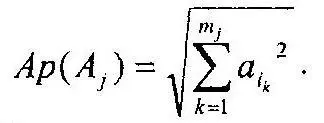
При этом разложение множества А jна сумму взаимно не пересекающихся множеств эквивалентно разложению вектора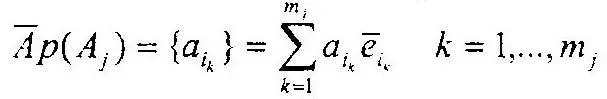

на сумму взаимно ортогональных векторов, каждый из которых имеет координаты, равные амплитудам элементарных событий, входящим в множество, которое он характеризует, е j— орт координаты, характеризующей i-й элементарный возможный исход бифуркационного события.

Формула Байеса переписывается в терминах амплитуды вероятностей следующим образом:

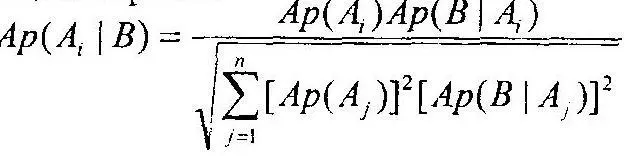
Пусть дана однозначная функция s(ω) исхода бифуркационного события ω. Тогда функция Р s, определённая формулой Р s(А) = Р{s -1(A)}называется вероятностной функцией s, а функция АР sамплитудой вероятностной функции s.

Функция F s(S) = Р s(-бесконечность, S) = Р {s(ω) < S} называется функцией распределения случайной величины s.

Если свойства состояний системы являются периодическими функциями от s, с периодом h, то назовём величину s действием и вместо величины s введём спиральную переменную, путём отображения прямой линии s на цилиндрическую круговую спираль с основанием цилиндра единичного радиуса.

Точка на этой спирали может быть описана спиральным комплексным числом с единичным модулем e 2ms/h. Проекцией каждого такого числа на комплексную плоскость является точка на окружности единичного радиуса, описываемая алгебраическим комплексным числом e iθ.

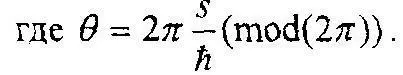
Как величина действия s. так и величина периода действия h, могут быть приняты в качестве параметра целого при исследовании системы на ранних стадиях.

Следующим шагом в анализе бифуркационного события является введение в рассмотрение, по аналогии с действительным вектором вероятности, комплексного волнового вектора Ψ.

Рассмотрим первоначально компоненты этого вектора. Каждому элементарному исходу бифуркационного события (каждому элементу ω i) сопоставим единичный вектор e jнаправленный вдоль оси абсцисс комплексной плоскости z i.. В этом случае можно ввести собственный волновой вектор данного исхода бифуркационного события