Г. Басина - Синергетика. Основы методологии

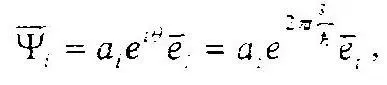
принимающий значения в любой точке единичного круга комплексной области z i, включая его центр (в случае невозможности данного исхода) и окружность единичного радиуса (в случае неотвратимости наступления события). Наряду с этим вводим единичный комплексный собственный вектор.

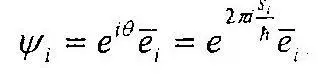
Сумма комплексных волновых векторов для всего конечного множества возможных исходов формирует полный волновой вектор бифуркационного события, или волновой вектор возможных состояний системы.

В синергетической методологии существенную роль играют логарифмы вероятностей исходов бифуркационного события, совокупность которых для данной системы можно представить в виде собственных чисел некоторого оператора, названного нами оператором энтропии.

Осреднение собственных чисел оператора энтропии по всему пространству возможных исходов бифуркационного события позволяет получить некоторое число, которое может быть названо энтропией будущего этого события.

Это число даёт общее представление о степени неопределённости исходов бифуркационного событии и является важной характеристикой исследуемой системы.

Однако, величина энтропии зависит от нашего произвола в выборе вариантов элементарных исходов события, особенно в случае, если пространство возможных исходов представляет собой континуум. Поэтому этот параметр должен быть использован достаточно осторожно.

Более разумно принять несколько вариантов разбиений пространства возможных исходов события.

Для каждого варианта разбиения можно подсчитать своё значение энтропии и максимальное её значение, соответствующее равномерному распределению вероятностей различных вариантов исходов.

Различие между полученным значением энтропии для данной системы и максимальным её значением при данном числе разбиений характеризует доступную нам информацию о возможном поведении системы.

В качестве пространства разбиений для системы, поведение которой нельзя считать детерминированным, можно на первом этапе исследований принять область значений параметра целого. Если поведение системы с некоторым приближением можно считать детерминированным, то энтропия события, в котором участвует система, может быть принята равной нулю, и мы можем вернуться к исследованию объекта как детерминированной динамической системы.

При вычислении энтропии бифуркационного события необходимо рассматривать несколько возможных вариантов.

Первый вариант соответствует наличию дискретного набора возможных состояний системы после совершения события. Если вероятности каждого из вариантов заданы или определены эмпирически, то энтропия события определяется однозначно.

В случае, если возможные исходы бифуркационного события до его свершения составляют континуум и плотность вероятности является гладкой функцией от меры, такой подход невозможен, так как величина энтропии зависит от числа разбиений континуального множества и стремится к бесконечности при увеличении числа элементов разбиения. Однако в этом случае энтропия события может быть представлена в виде двух составляющих, одна из которых стремится к бесконечности, сохраняя универсальный закон зависимости от числа разбиений, а другая в пределе не зависит от числа разбиений, а лишь от формы кривой распределения плотности вероятности по пространству возможных состояний. Эту последнюю часть и можно принять за энтропию события в этом случае.

После свершения бифуркационного события система оказывается в некотором определённом состоянии. Её энтропия обращается в нуль. А наблюдатель получает количество информации, равное энтропии события до его свершения.

У исследуемой системы можно выделить два характерных типа поведения.

Периоды сравнительно плавных изменений, когда система может быть приближённо описана как детерминированная и для её описания пригодны методы теории динамических систем (русла в терминологии Г.Г.Малинецкого). Этим периодам соответствуют рёбра графа структур и событий.

Периоды резких бифуркационных изменений — бифуркационные события — (джокеры в терминологии Г. Г. Малинецкого), в результате которых система может оказаться не в одном детерминированном, а с различной степенью вероятности в каждом из спектра возможных состояний, выбор одного из которых заранее не предрешён.

Приближённое графическое представление последовательности связанных между собой бифуркационных событий, которые уже произошли и которые ещё могут произойти, мы назвали графом структур и событий.

В графе структур и событий особо следует выделить текущий момент времени.

Позади него прошлое, события в котором уже свершились, впереди — будущее, которое должно быть предсказано с той или иной степенью вероятности. Предсказание будущего, получение знания о будущем — основная задача исследователя.

При анализе графа целесообразно выделить в качестве опорных два предельных случая.

Пусть система устроена таким образом, что после каждого бифуркационного события она может оказываться только в новых состояниях, отличных от предыдущих. Причём, время и относительные вероятности реализации этих состояний известны.

Граф становится «математическим деревом».

Вероятность и амплитуду вероятности для каждого состояния в будущем можно вычислить как произведение относительных вероятностей или амплитуд по единственному пути, ведущему к данному состоянию в соответствии с рассмотренными выше формулами элементарной теории вероятностей.

Если мы знаем, в каком состоянии оказалась система в данный момент, то можем определить не только всю цепочку бифуркационных событий, которую она прошла, но и все их исходы. Поэтому такой граф назван нами графом с бесконечной памятью.

Однако, определение относительных вероятностей и моментов свершения будущих бифуркационных событий представляет отдельную задачу, решение которой относится к проблеме получения знаний. В случае графа с бесконечной памятью она практически неразрешима, если знания о будущем не даны нам априори.

В этом случае появляется зависящая от времени матрица вероятностей перехода из одного состояния в другое при совершении серии бифуркационных событий. Если бифуркационные события происходят регулярно, то могут быть рассчитаны асимптотические статистические распределения вероятностей и определено асимптотическое значение энтропии системы в будущем.