Леонард Сасскинд - Битва при черной дыре. Мое сражение со Стивеном Хокингом за мир, безопасный для квантовой механики

Здесь-тο и появляется антидеситтеровское пространство (АДС). Прежде всего, надо отметить, что, несмотря на свое название, антидеситтеровское пространство в действительности является пространственно-временным континуумом, одним из измерений которого служит время. Виллем де Ситтер был голландским физиком, математиком и астрономом, который открыл четырехмерное решение уравнений Эйнштейна, носящее его имя. Математически пространство де Ситтера — это экспоненциально расширяющаяся вселенная, которая растет во многом подобно тому, как это проис- [147] В последние годы астрономы и космологи обнаружили, что наша Вселенная расширяется в ускоренном темпе, удваивая свой размер примерно за десять миллиардов лет. Это экспоненциальное расширение связывают с космологической постоянной, или «темной энергией», как ее называют в популярной прессе. ходит с нашей реальной Вселенной [147] В последние годы астрономы и космологи обнаружили, что наша Вселенная расширяется в ускоренном темпе, удваивая свой размер примерно за десять миллиардов лет. Это экспоненциальное расширение связывают с космологической постоянной, или «темной энергией», как ее называют в популярной прессе. . Пространство де Ситтера долгое время считалось не более чем математической диковиной, но в последние годы оно приобрело огромное значение для космологов. Это искривленный пространственно-временной континуум с положительной кривизной, то есть сумма углов треугольника в нем больше 180 градусов. Но все это к делу не относится. В этот раз нас интересует не пространство де Ситтера, а антидеситтеровское пространство.

Антидеситтеровское пространство не было открыто антиматериальным двойником де Ситтера. Приставка «анти» указывает на то, что кривизна этого пространства отрицательная, а значит, сумма углов треугольника меньше 180 градусов. Самая интересная особенность АДС состоит в том, что оно обладает многими свойствами внутреннего пространства сферической шкатулки, но такой, которая не может быть проглочена черной дырой. Дело в том, что сферические стены АДС наделены мощной силой — непреодолимым отталкиванием, действующим на все, что к ним приближается, включая и горизонт черной дыры. Это отталкивание столь сильное что контакт между стенкой и черной дырой совершенно невозможен.

Обычное пространство-время имеет четыре измерения — три пространственных и одно временнóе. Физики иногда называют его четырехмерным, но это скрывает различие между пространством и временем. Более точно описывать пространство-время как (3 + 1) — мерное.

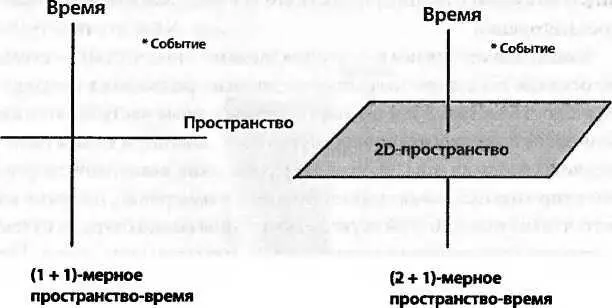
Флэтландия и Аайнландия — это тоже пространственно-временные континуумы. Флэтландия — мир лишь с двумя измерениями пространства, но его обитатели имеют чувство времени. Они должны корректно описывать свой мир как (2+1) — мерный. Лайнландцы, которые могут двигаться только вдоль одной оси, но также ощущают время, живут в (1 + 1) — мерном пространстве-времени. Замечательная особенность размерностей (2+1)и(1 + 1) состоит в том, что мы легко может изображать такие пространства на картинках, что помогает нашей интуиции.

Конечно, ничто не мешает математическим физикам изобретать миры с любым числом пространственных измерений, несмотря на неспособность мозга их визуализировать. Однако интересно, можно ли изменить число временных измерений? В чисто абстрактном математическом смысле ответ — да, но он, похоже, не имеет большого смысла с физической точки зрения. Одно измерение выглядит вполне подходящим значением.

Антидеситтеровские пространства могут быть разной размерности. У них может быть любое число пространственных направлений, но только одно временнбе. То АДС, с которым работали Банадос, Тейтельбойм и Занелли, было (2 + 1) — мерным, что позволяет легко все объяснить на картинках.

Трехмерное пространство (не пространство-время) — это одна из тех вещей, которая кажется жестко прошитой в нашей когнитивной системе. Никто не может визуализировать четырехмерное пространство без опоры на абстрактную математику. Может показаться, что одно- и двумерные пространства изобразить проще, и, в определенном смысле, так и есть. Но если вы на мгновение задумаетесь, то поймете, что, визуализируя линии и плоскости, вы всегда представляете их вложенными в трехмерное пространство. Это почти наверняка связано с тем, как эволюционировал наш мозг, и не имеет никакого отношения к особым математическим свойствам трех измерений [148] Может ли физический мир быть одно- или двумерным (я имею в виду пространство, не пространство-время)? Я твердо не знаю — нам известны не все принципы, от которых это может зависеть, — но с математической точки зрения квантовая механика и специальная теория относительности остаются столь же непротиворечивыми в одном и двух измерениях, как и в трех. Я не утверждаю, что в этих альтернативных мирах может существовать разумная жизнь, а лишь говорю, что некоего рода физика в них возможна. .

Квантовая теория поля — теория элементарных частиц — столь же осмысленна в мире с меньшим числом измерения, как в трехмерном пространстве. Судя по всему, элементарные частицы вполне возможны в двумерном пространстве (Флэтландии) и даже в одномерном (Аайнландии). Фактически уравнения квантовой теории поля упрощаются, когда уменьшается число измерений, и многое из того, что мы знаем об этой науке, было первоначально открыто путем изучения квантовой теории поля в подобных модельных мирах. Так что ничего необычного в том, что Банадос, Тейтельбойм и Занелли изучали вселенную всего с двумя измерениями, не было.

Лучший способ объяснить АДС — тот, что предложил Клаудио во время чилийской автобусной экскурсии: на картинках. Не будем пока думать о времени и начнем с обычного пространства внутри пустой круглой шкатулки. В трех измерениях ее внутренняя область будет сферической; в двух измерения она еще проще и имеет форму круга.

Теперь добавим время. Когда оно отложено по вертикальной оси, пространственно-временной континуум напоминает внутреннюю область цилиндра. На рисунке АДС — это незакрашенная внутренность цилиндра.

Представим себе срезы АДС (напоминаю, они имеют два измерения) по аналогии с тем, как мы нарезали черную дыру при построении диаграммы вложения. Нарезание выделяет сечения, о которых можно сказать, что они именно пространственные.