Мартин Гарднер - Когда ты была рыбкой, головастиком - я...

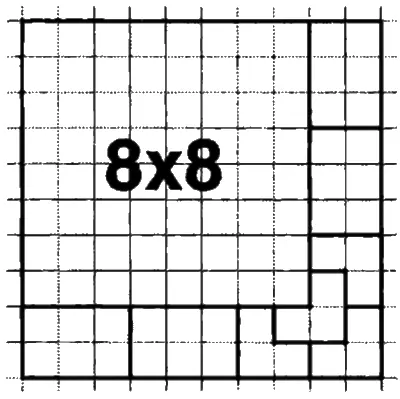
Обычно труднее всего покрыть доски, у которых длина сторон — простое число. Проблему доски 17-го порядка удается решить, поместив в ее угол квадрат со стороной 13 и оставив внизу и сбоку область шириной 4. Проблему доски 19-го порядка — поместив в ее угол квадрат 14-го порядка (доказательство его покрываемости основано, в свою очередь, на таком же свойстве квадрата 7-го порядка) и получив угловую область шириной 5 (см. рис. 8).

ПОЛНЫЙ И УНИВЕРСАЛЬНЫЙ РЕЗУЛЬТАТ

Занимаясь разбиением этих фигур, я подобрался (но пока недостаточно близко) к тому, чтобы вывести индуктивное доказательство того, что все дефицитные квадраты покрываемы, за исключением квадрата 5-го порядка. Это доказательство в конце концов получили И. Пинг Чу и Ричард Джонсонбау [77] L.P. Chu and R. Johnsonbaugh, «Tiling deficient boards with trominoes», Mathematics Magazine 59:34–40,1986. . Чу и Джонсонбау позаботились не только обо всех дефицитных квадратах, но и обо всех дефицитных прямоугольниках! Их индуктивное доказательство — слишком специальное, чтобы его здесь приводить. Коротко говоря, они продемонстрировали покрываемость для всех прямоугольников m×n (включая и квадраты — случай, когда m=n) с числом клеток, кратным 3 после удаления одного поля. Подобные доски покрываемы, если выполняются все четыре необходимых и достаточных условия:

1) m ≥ 2,

2) n ≥ m,

3) если m=2, n должно тоже равняться 2,

4) m ≠ 5.

Прямоугольник 4×7 — самый маленький дефицитный прямоугольник (не квадрат), который можно покрыть с помощью L-тримино. Вот еще одно упражнение: много ли у вас уйдет времени на то, чтобы покрыть такую фигуру с помощью тримино и двух элементов 2×3, если недостающая клетка у этой фигуры располагается в углу?

Кристофер Йенсен показал в своей неопубликованной статье, что если в углу любой доски убрать две клетки, как показано на рис. 9. получившуюся доску нельзя будет покрыть с помощью тримино. Однако, если исключить приведенные пять случаев, доску с длинами сторон 3m–1 и 3n+1 и с любыми двумя недостающими клетками окажется возможным покрыть при следующем необходимом и достаточном условии: либо если n=1, либо если m ≥ 3 и n ≥ 3.

Заключение

Кейт Джонс, основавшая и возглавляющая фирму «Kadon Enterprises», которая выпускает и продает разные симпатичные механические головоломки и другие забавные математические предметы, выпустила на рынок игру под названием «V-21» [78] K. Jones, Vee-21 available at www.gamepuzzles.com/polycub2.htm#V21. . Буква V здесь — от «V-тримино», а 21 — число тримино в наборе, где кроме ярко раскрашенных фишек имеется также доска 8-го порядка, на которую их можно класть. Первое задание — положить мономино (квадрат 1-го порядка) в произвольное место доски, а затем покрыть оставшуюся площадь с помощью тримино (т. е. решить задачу для доски 8-го порядка). К игре прилагается сорокастраничное руководство. В нем напечатана короткая статья Нортона Старра «Дефицитная шахматная доска» и приводятся изображения прямоугольных досок и задачи к ним.

Завершим наш рассказ красивейшим симметричным покрытием стандартной шахматной доски (рис. 10).

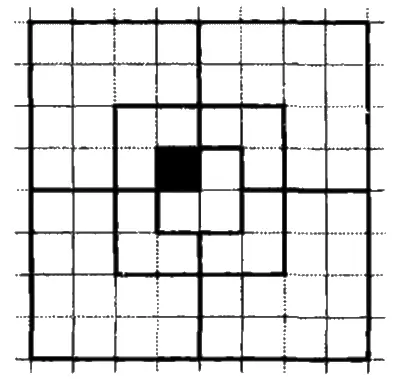
А вот и ответ на задачу, которую я предложил вам на с. 197:

Рубен Херш принадлежит к небольшой группе математиков, убежденных, что математика реальна лишь в контексте человеческой цивилизации. А я — бесстыжий платоник и предпочитаю иной язык мышления, предполагающий, что если из Вселенной исчезнут все разумные существа, то математические объекты и теоремы в каком-то смысле никуда не денутся — даже если не останется никого, кто смог бы писать или говорить о них. Гигантские простые числа продолжают быть простыми, хоть никто и не доказывал, что они являются таковыми. Как выразился однажды Бертран Рассел, даже в центре Солнца дважды два — четыре.

Более ранние мои замечания по этой теме см. под заголовком «В защиту платоновского реализма» — так называется глава у моей книги «Джинн из гиперпространства» (Амхерст, штат Нью-Йорк: «Prometheus Books» , 2008).

Брайан Дэвис в своей статье «Дайте платонизму умереть» («IMS Newsletter» [79] «Бюллетень «Intelligent Manufacturing Systems»». , июнь 2007) определяет математический платонизм как убежденность в том, что математические объекты существуют «в некоем математическом царстве, за пределами времени и пространства». Но у меня (как, полагаю, и у большинства математических платоников) — иные убеждения. Аристотель, математический реалист, с радостью ухватился за платоновские универсалии трансцендентального царства («оранжевость», «коровность», «двоечность» и т. п.), приспособив их к объектам, существующим во времени и пространстве. Так, геометрическая форма вазы находится «здесь», в данной вазе, эта форма не плавает где-то возле платоновской «пещеры».

В качестве примера можно рассмотреть камешки. Пусть каждый из них — модель числа 1. В таком случае очевидно, что все теоремы арифметики можно доказать, перекладывая камешки. В принципе таким путем можно даже доказать, что произвольно выбранное число (не важно, насколько большое) является простым или составным.

Рубен Херш, мой давний оппонент, в своей статье «О платонизме» пишет:

На мой взгляд, платонизм (имея в виду обычный, бытовой платонизм типичного практикующего математика) справедливо признаёт существование математических фактов и объектов, не управляемых волей или прихотью конкретного математика, но обрушиваемых на него как объективные факты и сущности, о которых он должен узнавать и чье независимое существование и чьи качества он стремится обнаруживать и исследовать.

Что ж, профессор Херш, добро пожаловать в Платоновский клуб! Любой платоник всецело согласится с вашими словами. Но затем Херш делает невероятное заявление: «Ошибка платонизма — в неверной интерпретации этой объективной реальности, в выведении ее за рамки человеческой культуры и сознания».