Марат Телемтаев - Целостный метод системной технологии и системная экология

≤ μ ( i ki k+2 ) + μ ( i k+2i k+1 ) + μ ( i k+1i k+3 ).

Условие (2) необходимо проверить для всех i k = i 1, i 2, …, i n и, если оно для всех i k справедливо, то это необходимое и достаточное условие того, что гамильтонов цикл 4-оптимален. Просуммировав левые и правые части неравенств, получающихся при значениях i k = i 1, i 2, …, i n, получаем необходимое условие 4-оптимальности в виде:

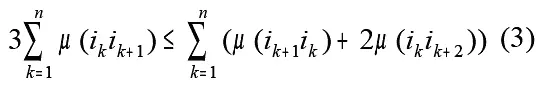
Справедливо следующее условие:

Если гамильтонов цикл a 1- оптимален, то он a 2 -оптимален для любого a 21.

Если это условие не выполняется, т.е. a 1- оптимальный гамильтонов цикл не является a 2 -оптимальным, то какой-то из простых путей длины a 1 можно улучшить изменением обхода каких-то a 2 вершин, что противоречит условия a 1 -оптимальности.

Перейдем к определению условия a -оптимальности, получаемого аналогично тому, как условие (З) получено из (2), из системы неравенств вида (2), для любого a=const суммированием для всех i k=1, 2, …, n

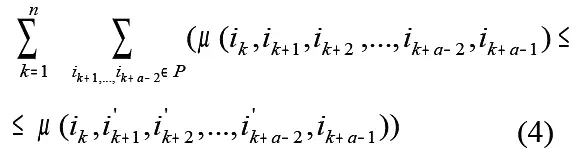
Для каждого значения k будет иметь место система из ((а-2)!-1) неравенств по числу элементов множества Р , состоящего из ( а-2 ) ! перестановок чисел i΄ k+1 , i΄ k+2 , …, i΄ k+a-2

При этом мы полагаем, что

μ ( i k,i k+1 , …, i k+a-1 ) = μ ( i k, i k+1 ) + μ ( i k+1i k+2 ) + … + μ ( i k+a-2i k+a-1 ).

μ ( i k, i΄ k+1 , …, i΄ k+a-2 , i k+a-1 ) = μ ( i k, i΄ k+1 ) + μ ( i΄ k+1 , i΄ k+2 ) + … + μ ( i΄ k+a-2 , i k+a-1 ).

Обозначим левую и правую части условия (4) буквами А и В, соответственно: А ≤ В.

В левой части неравенства вес каждого ребра, принадлежащего проверяемому участку гамильтонова цикла, участвует точно по одному разу в каждом неравенстве системы из (( a-2 ) !-1 ) неравенств, задаваемых перестановками, принадлежащими множеству Р , при фиксированной начальной вершине.

Кроме этого, при заданном a=const , если производить проверку выполнения условия (9.2.4), изменяя последовательно номер начальной вершины от i 1 до i n, то любое ребро гамильтонова цикла появится точно в ( a-1 ) системах из этих (( a-2 ) !-1 ) неравенств как первое по счету, второе, третье и т.д. ( a-1 ) -e ребро в проверяемых участках гамильтонова цикла.

Следовательно, левая часть неравенства (4) имеет вид:

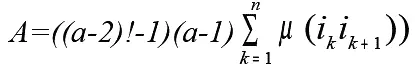
Выражение для правой части условия (4) можно записать в виде:

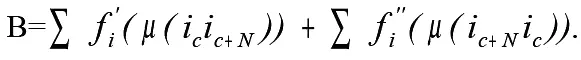
Для того, чтобы получить выражение для правой части условия (4), необходимо найти число появлений ребер графа вида ( i c, i c+N ) в каждой системе из (( a-1 ) !-1 ) неравенств, задаваемых определенным значением k ,а также во всех системах этих неравенств, получаемых при изменении i k от i 1 до i n .

Очевидно, что число появлений пар ( i с, i c+N ) в правых частях неравенств вида (4) равно числу появлений пар ( i c, i c+N ) в последовательностях:

i k, i΄ k+1 , i΄ k+2 , …, i΄ k+a-2 , i k+a-1 (5)

задаваемых ( a-2 ) ! перестановками чисел i΄ k+1 , i΄ k+2 , …, i΄ k+a-2 .

Следует учесть также, что одна из этих последовательностей, а именно i 1, i 2, i 3, …, i k+a-1 находится в левой части этих неравенств.

Пары i ci c+N можно разделить на следующие виды по признаку, содержат они или нет «неподвижные» вершины i k и i k+a-1 :

а) i ci c+N при c ≠ k; c + n < k+a-1; n > 1, n ≤ a-2; это пары элементов в (5), не содержащие элементов i k, i k+a-1 и тех элементов ( i 1, i 2, i΄ 2, i 3, i΄ 3, i 4 и т.д.), которые входят в гамильтонов цикл (1a).

Каждая из пар этого вида появится в системе неравенств (4) для определенного значения i k=i 1,i 2, …, i n , точно ( a-3 )( a-4 ) ! раз – по числу ( a-4 ) ! перестановок ( a-4 ) элементов, т.е. элементов последовательности (5) за вычетом элементов i k, i k+a-1, i c, i c+N для каждого из ( a-3 ) возможных положений пары i c, i c+N в последовательности (5).

б) i c, i c+N при n>1, c=k и i c+Ni c+a-1 при n < а-2, c=k это пары элементов в (5), содержащие элементы i k или i k+a-1 и элементы гамильтонова цикла (1a).

Каждая из этих пар появится в системе неравенств (4) для определенного значения i k=i 1,i 2, …, i n, точно ( a-3 ) ! раз по числу возможных перестановок ( a-3 ) элементов, т.к. элементы i k, i k+N, i k+a-1 для этих пар «неподвижны».

Кроме этого, в совокупностях пар обоих видов надо выделить пары i c, i c+1, т.е. пары элементов гамильтонова цикла (1а). Тогда можно считать, что каждая из этих пар появится в системе неравенств (4) для определенного значения i k=i 1,i 2, …, i n точно (( a-3 ) !-1 ) раз по числу появлений пар вида а) или б) и за вычетом появлений одной пары, находящейся в левой части неравенства (4).

Аналогично и для любой пары вида i с+Ni с число появлений в системе неравенств (4) для определенного значения i k равно ( a-3 ) !. З десь надо учесть то обстоятельство, что i k и i k+a-1 «неподвижны», т.е. они не могут участвовать в парах вида i с+Ni с.

Таким образом, каждая пара элементов вида i сi с+N , не образующая ребро, инцидентное гамильтонову циклу, а также каждая пара вида i с+Ni с появятся в правой части системы неравенств, записанных для определенного значения i k , точно ( a-3 ) ! раз, а ребра, инцидентные гaмильтонову циклу, точно (( a-3 ) !-1 ) раз.

Задавая последовательно значения i k от i 1 до i n, мы получаем каждый раз новые системы неравенств. При этом относительно любого ребра i c, i c+N участок i k, i k+1, …, i k+a-1 «передвигается», вследствие чего любые пары i c+Ni c или i c, i c+N участвуют в a-N ( k+a-1-n-k+1=a-N ) системах неравенств (4) .То обстоятельство, что пары вида ( i c+N, i c ) с участием элементов i k и i k+a-1 в каждой системе неравенств невозможны, приводит к уменьшению числа появлений каждого такого вида пар i c+Ni c в системе (4) для данного N на две.

Ребра i ci c+1 участвуют, таким образом, в ( a-1 ) системах неравенств, если, конечно , ( a-3 ) !-1 ≥ 1 или a ≥ 5, т.е., если они по условию вообще появляются в правой части системы неравенств для любого i k.

Отсюда очевидно, что любое ребро μ ( i ki k+N ), N ≠ 1, графа будет повторяться в правых частях n систем неравенств (4) ( a – N ) раз для i k= i 1 , i 2, …, i n .