Владимир Кирсанов - Научная революция XVII века

Решение Кеплером этой задачи Альберт Эйнштейн (из статьи которого о Кеплере взяты эти строки) считает одним из крупнейших достижений науки, поистине заслуживающим восхищение. Кеплер воспользовался Марсом в качестве «своеобразного триангуляционного пункта», с помощью которого оказалось возможным определить орбиту Земли. Действительно, предположим, что Марс занимает некоторое неподвижное положение М в плоскости земной орбиты. Тогда легко определить направление SM (Солнце — Марс) относительно неподвижных звезд. Для этого нужно лишь отметить то положение, когда Земля, Солнце и Марс лежат на одной прямой, что несомненно произойдет в некоторый момент времени. В другой момент времени Земля уже не будет лежать на прямой SM, а будет находиться в некоторой точке T 1своей орбиты. Для этого момента также можно определить направление ST 1и T 1M относительно неподвижных звезд. Тогда в треугольнике SMT 1будут известны все углы и одна сторона MS неизменна— ее величину можно выбрать произвольно, и, следовательно, в выбранном масштабе можно получить расстояние T 1M (Марс — Земля). Эту процедуру можно повторить для любого момента времени, получив достаточное число точек для определения земной орбиты.

Однако, как мы знаем, Марс не является неподвижным, но движется вокруг Солнца. И тем не менее Кеплер сумел использовать описанную схему, найдя гениально простое решение. Известно, что Марс обращается вокруг Солнца за вполне определенное время, его период равен 687 суткам, поэтому если за начало отсчета выбрать момент, когда Марс, Солнце и Земля лежат на одной прямой, то следующая точка наблюдения должна отстоять по времени от первой на 687 суток. За это время Марс вернется в свое первоначальное положение, а Земля займет некоторое другое положение, отличное от первого. Следующее положение Земли определится временем, равным двум периодам Марса, и т. д.

Поступая таким образом, Кеплер смог определить движение Земли. Но не следует думать, что Кеплер получил в результате эллиптическую орбиту, хотя такое впечатление может сложиться при чтении многих популярных статей и книг о Кеплере. На самом деле вследствие очень малого эксцентриситета земной орбиты Кеплер не смог установить, что орбитой Земли является эллипс, и по-прежнему считал, что она представляет собой окружность. Тем не менее он был в состоянии с достаточно хорошей точностью определить скорость Земли на орбите в зависимости от ее местонахождения на ней. В частности, он показал, что скорость движения Земли неодинакова для разных частей орбиты, поэтому теорию движения Земли следует строить аналогично тому, как это делается для других планет.

До исследований Кеплера была повсеместно принята та точка зрения, что Земля в отличие от других планет движется равномерно по орбите;, в то время как для других планет Птолемеем было введено понятие экванта — точки, из которой неравномерное движение планеты кажется равномерным. Кеплер показал, что движение Земли также находится в согласии с гипотезой экванта, являясь, по сути, неравномерным. Он предположил, что орбита Земли должна быть эксцентрической (по отношению к Солнцу) окружностью, центр которой делит пополам линию, соединяющую Солнце с центром равноуглового движения (эквантом). Более того, он показал, что вблизи апсид [3] Линия апсид соединяет наиболее удаленную от Солнца точку орбиты — афелий с наиболее близкой к нему точкой — перигелием. Одним из важных достижений Кеплера было осознание того факта, что эта линия проходит через Солнце. О. Гингерич предложил даже называть это положение «нулевым законом Кеплера». время, затрачиваемое Землей на прохождение равных дуг орбиты, пропорционально расстоянию от Солнца. Затем Кеплер без колебаний распространил эту закономерность на всю орбиту.

Запомним эту первую гипотезу Кеплера на пути к созданию закона площадей: время пропорционально расстоянию от Солнца. Чтобы эта гипотеза в его собственных глазах выглядела правдоподобной, Кеплер должен был наполнить ее неким физическим содержанием. Согласно его представлениям, источником движения планет является Солнце, которое, вращаясь, испускает потек особых частиц (species immateriata), которые, сталкиваясь с планетой, движут ее по окружности. Однако поток таких частиц может обусловить лишь движение по такой окружности, у которой Солнце располагается в центре. Чтобы объяснить движение планеты по окружности, эксцентрической по отношению к Солнцу, Кеплер наделяет планету собственной способностью взаимодействия с потоком (species immateriata), которая дает ей возможность то удаляться, то приближаться к Солнцу. Действие этой способности, или силы («интеллигенции»), планеты аналогично действию руля у лодки: в зависимости от поворота руля лодка может плыть под различным углом к течению реки.

Кеплер пытался детально объяснить механизм действия собственной силы планеты с помощью модели, использующей движение по эпициклу и деференту (такая модель, как мы указывали ранее, эквивалентна модели эксцентрической окружности), но немедленно столкнулся с проблемой, решить которую был не в состоянии: как сила может двигать планету (и при том неравномерно!) вокруг центра, существующего лишь в воображении? Кеплеру было очевидно, что модель Птолемея не может здесь быть путем к объяснению, а другого пути пока он не видел. Отложив на время детали физического объяснения, он удовлетворился тем, что принял, что движение планет обусловлено двумя силами — силой, исходящей от Солнца посредством действия species immateriata, которая движет планету по окружности с Солнцем в центре, и собственной силой планеты, которая корректирует первоначальное движение таким образом, что планета начинает двигаться по окружности, эксцентрической по отношению к Солнцу.

Удовлетворившись на время этим вариантом физического объяснения, Кеплер обратился к проверке своей первой гипотезы (время пропорционально расстоянию), распространенной на всю орбиту Земли, путем сравнения расчетных и наблюденных значений истинной аномалии. [4] «Истинная аномалия» — угол между линией апсид и радиусом-вектором, проведенным от Солнца к планете. Кеплеру было чуждо понятие мгновенной скорости, и в соответствующих местах он всегда говорит о времени, требуемом для прохождения данной дуги, точно так же: время для него всегда представлялось не непрерывно текущей координатой, а последовательностью конечных временных промежутков (в полном соответствии с традицией средневековой физики).

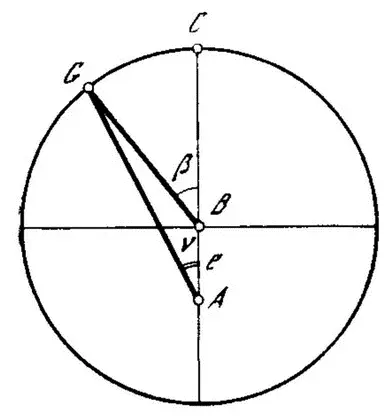
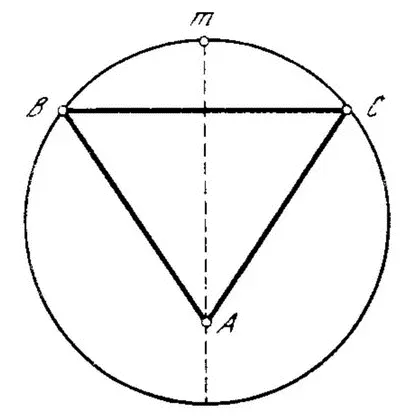
Поскольку время пропорционально расстоянию, то любой промежуток времени, согласно Кеплеру, будет измеряться суммой всех расстояний, содержащихся в секторе соответствующей дуги. Затем рассуждения Кеплера можно представить следующим образом. Пусть окружность разделена на 360 равных частей, так что каждому элементарному углу Δβ i(эксцентрической аномалии), равному π /180, соответствует расстояние r iот Земли до Солнца. Тогда время, потраченное планетой на перемещение β от афелия до любой точки G, относится ко времени полуоборота как сумма расстояний, содержащихся в эксцентрическом секторе GAC, к сумме расстояний, содержащихся в половине эллипса, т. е.