Владимир Кирсанов - Научная революция XVII века

Другим результатом подобного рода было знаменитое «мертонское правило», определяющее возможность сопоставления равномерного и равноускоренного движений. В формулировке Суиссета это правило гласит: «Всякая широта движения, униформно приобретаемая или теряемая, соответствует своему среднему градусу, так что столько же в точности будет пройдено благодаря этой приобретаемой широте, сколько и благодаря ее среднему градусу, если бы тело двигалось все время с этим средним градусом» {2, с. 136}. Терминология Суиссета нуждается в пояснении — под «широтой» калькуляторы понимали интенсивность качества, а «градус», как и выше, есть мера этой интенсивности, значение которой может изменяться от нуля до бесконечности. Поэтому теория усиления и ослабления качеств называлась также учением о «широте форм», где под «формой» подразумевалось некое качество, подлежащее рассмотрению, Имея в виду эти соображения, мертонское правило можно интерпретировать таким образом, что путь, пройденный во время равноускоренного движения, равен пути, проходимому в равномерном движении со средней скоростью.

Результаты ученых Оксфордской школы, пользовавшихся языком словесной алгебры, чтобы математизировать учение об интенсивности качеств, были переформулированы на более наглядном и потому более понятном языке в трудах парижских ученых. В этом предприятии основная заслуга принадлежит Никола Орему.

Около 1350 г. им был написан «Трактат о конфигурации качеств и движения» [10] См. подробнее: Зубов В. П. Трактат Николая Орема «О конфигурации качеств» // Историко-математические исследования. М.: Наука, 1958. Вып. 11. С. 601—731. , в котором используется другой по сравнению с трудами калькуляторов подход к проблеме. Интенсивность любого качества, согласно Орему, можно изобразить в виде отрезка прямой, и если место (extensio) мыслить как долготу (longitudo) на горизонтальной прямой, тогда интенсивность (intensio) любой точки будет изображаться соответствующим вертикальным отрезком прямой, а зависимость интенсивности от места (точки) — множеством таких отрезков. Верхние концы отрезков будут тогда располагаться на некоторой кривой, которая и определяет «конфигурацию» качества. Конфигурации означали у Орема качество как целое, причем ценность качества зависит от красоты конфигурации.

Хотя графическое представление интенсивностей у Орема очень похоже на современное использование системы координат для изображения функциональной зависимости, у него не было понятия о. системе координат как таковой — речь в его трактате шла лишь о расстояниях между точками и отрезками прямой. Тем не менее «графический метод Орема предполагал понимание функциональной зависимости; эту идею можно найти во множестве его работ, и она никоим образом не была необычной для середины четырнадцатого столетия» {1, с. 64}.

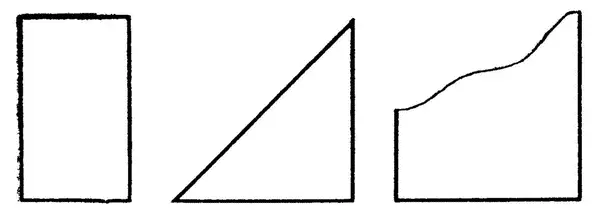
Во второй части своего трактата Орем рассматривает движение; в этом случае долгота соответствует времени, а интенсивность — скорости. Тогда получается, что равномерному движению соответствует постоянная интенсивность и конфигурацией, отражающей его, является четырехугольник; аналогично конфигурацией равноускоренного движения будет треугольник или прямоугольная трапеция (в зависимости от того, отличается или нет начальная скорость от нуля).

В третьей части обсуждается проблема эквивалентности движений, и Орем приходит к мертонскому правилу: униформно-дифформное движение эквивалентно униформному движению со средней скоростью, основываясь на предположении, что движения эквивалентны, если площади их конфигураций равны. Равенство соответствующих конфигураций он доказывает с помощью конгруэнтных треугольников, и мертонское правило получает, таким образом, ясный геометрический смысл. Отметим, что Орем не сделал следующий шаг и не применил свой чертеж к исследованию проблемы падения, что спустя два с половиной столетия сделал Галилей, который, впрочем, исходил из совершенно других, чем Орем, предпосылок.

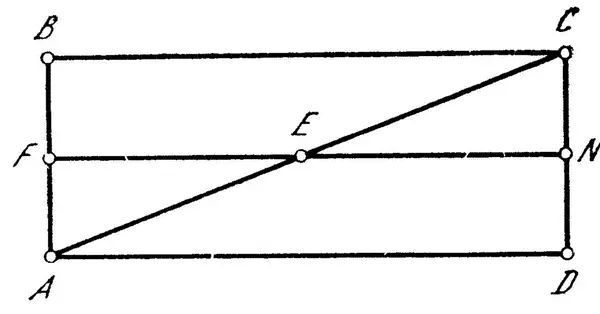
Заслуживает внимания представление Орема о площади фигуры как о мере пройденного пути. Он использует это представление при обсуждении мертонского правила, а в дальнейшем применяет его к доказательству двух важных положений: можно представить движение, в котором скорость бесконечно растет, но пройденный путь является при этом конечным; возможно также движение, длящееся бесконечно долго, при котором проходится конечный путь.

Возможность графического изображения, показанная Оремом, обусловила более ясное понимание характера непрерывного изменения и облегчило в дальнейшем введение понятия функции.

Перейдем теперь к теории импетуса, роль которой в эволюции физической мысли трудно переоценить. Однако чтобы эта оценка была адекватной, нам придется более детально остановиться на ключевых моментах теории, а также сделать несколько предварительных замечаний. Сразу же оговоримся, что средневековая теория импетуса рассматривается современной историей науки как отправная точка для развития новой теории, результатом которой было создание закона инерции, но при этом подчеркивается, что теория импетуса представляла собой независимый этап развития науки от аристотелевской к классической механике. Было бы неправильно рассматривать импетус как средневековый аналог закона инерции, как это делал, например, Пьер Дюэм в своих «Исследованиях по Леонардо да Винчи». Поэтому вопрос о сходстве и различии понятий импетуса и инерции потребует специального анализа. С другой стороны, необходимо иметь в виду, что современная терминология неадекватна: импетус не является ни силой, ни энергией, ни количеством движения в современном смысле, хотя и несет в себе черты каждого из этих понятий.

Проблема разделенного движения (motus separatus), которая привела в XIV в. к созданию теории импетуса, восходит к аристотелевскому принципу: «Все движущееся должно необходимо приводиться в движение чем-нибудь» {3, с. 124}. Этот принцип был усвоен и целиком разделялся схоластической натурфилософией, равно как и следующее из него положение, что любое движение предполагает наличие движущей силы, оно продолжается лишь в течение действия этой силы и заканчивается, как только сила перестает действовать. Все объяснения движения в случае разделенного движения (например, стрелы, пущенной из лука, или брошенного рукой камня) со времен Аристотеля сводились к тому, что передача движения от движителя к движимому телу обусловливалась через посредство среды. Таким образом, движитель передавал движение среде, сообщая ей движущую силу, которая затем преобразовывалась в движение снаряда. В такой трактовке «сила» понималась скорее как форма энергии.