Давид Ласерна - Эйнштейн. Теория относительности. Пространство – это вопрос времени.

Но возможен и обратный взгляд – на физику со стороны геометрии. Посмотрим на двумерное изображение Луны на ее орбите (рисунок 13).

Если мы сейчас задумаемся, как изобразить положение Луны в зависимости от времени, то интуиция нам подскажет: надо представить, как спутник описывает обороты вокруг нашей планеты. И воспринимая время как одну из пространственных характеристик, мы получим трехмерное геометрическое изображение движения Луны (рисунок 14).

Минковский ввел новое понятие – собственное время, обозначив его греческой буквой тау. Эта величина соответствует расстоянию не между двумя положениями тела, а между двумя событиями. Каждая совокупность координат включает в себя три пространственных значения и одно временное, определяя, где и когда произошло событие.

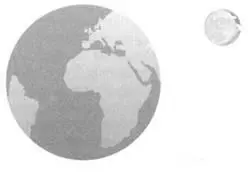
РИС. 13

РИС. 14

Два плоских изображения системы, состоящей из Земли и Луны, где пространство описывается только в двух измерениях.

На втором изображении (рисунок 14) добавляется время.

Перемещаясь из одной точки в другую, мы оставляем четырехмерный след – мировую линию. Нашу жизнь можно рассматривать как траекторию в пространстве Минковского, как последовательность мест и событий, связанных между собой. Мемуары физика Георгия Гамова так и называются – «Моя мировая линия: неформальная автобиография».

В предыдущей главе мы обнаружили, насколько пластично наше восприятие. Стоит только войти в зеркальный лабиринт относительности, перескакивая от одной системы отсчета к другой, как время и расстояние начинают вести себя, словно в декорациях сюрреалистического фильма, – они деформируются, растягиваются и сплющиваются. Движущиеся предметы сжимаются и замедляют ход своих часов. Однако собственное время продолжает быть расстоянием, то есть геометрическим свойством со всеми вытекающими последствиями. Таким образом, собственное время – это инвариант, предлагающий во всех системах отсчета, для любого наблюдателя одну и ту же информацию.

Если в евклидовом пространстве квадрат расстояния между двумя ближайшими точками (ds) определяется как ds² = dx² + dy² + dz² , то в пространстве Минковского аналогичный ему квадрат интервала равен ds² = dx² + dy² + dz² – c² dt² .

В результате умножения скорости света с (в международной системе она измеряется в м/с) на t (в секундах) четвертая переменная обретает ту же размерность, что и три пространственные переменные. Величина ds² инвариантна. Измерив ее в двух разных системах координат (х, у, z, t) и (х', у', z', t’), мы получим один и тот же результат:

ds² =dх² + dу² +dz² -c² dt²

=> c/s² =c/s'²

ds'² = dx'² +dy'² + dz'² – c² dt'²

Стремясь соединить две системы координат так, чтобы выполнялось равенство ds² = ds'² , мы приходим к уравнениям Лоренца. Извлечем метрическую функцию из формулы ds² :

В этом случае составляющие g с постоянными значениями образуют плоскость без каких-либо искривлений и неровностей. Ее геодезические линии прямые, но из- за изменения знака временной координаты они соответствуют не кратчайшей дистанции между двумя точками пространства-времени, а наиболее длинной.

Чтобы рассмотреть это подробнее, используем трехмерную параболу. Поставим стержень вертикально около стены и осветим его двумя прожекторами, сверху и сбоку. Тень, отбрасываемая благодаря вертикальному прожектору, будет иметь вид точки на полу, а с помощью бокового прожектора на стену упадет тень от всего стержня (рисунок 15).

Если теперь мы начнем наклонять стержень (в плоскости, определяемой двумя источниками света), то тень на полу будет расти, в то время как тень на стене – уменьшаться (рисунок 16).

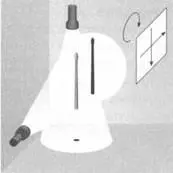
РИС. 15

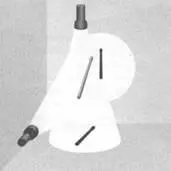
РИС. 16

РИС. 17

Переведя стержень в горизонтальное положение, мы увидим ситуацию, обратную начальной: тень на стене имеет вид точки, в то время как тень на полу равна всей длине стержня (рисунок 17).

Можно сказать, что пол и стена – это двумерные плоскости, обитатели которых могут наблюдать, как стержень укорачивается (в пространстве) и удлиняется (во времени). А мы получили геометрическую интерпретацию сжатия Лоренца и временного расширения. Обитатели наших двумерных поверхностей могли бы обеспокоиться, обнаружив, что длина стержня меняется при движении. Однако они могли бы разработать трехмерную математическую модель и прийти к выводу, что эти изменения иллюзорны. Во время движения стержня меняются исключительно размеры теней, а длина самого стержня в пространстве с большим количеством измерений остается неизменной.

В наших примерах используются как двумерные, так и трехмерные пространства. Между тем пространство Минковского нуждается в еще одном параметре: искривление пространства-времени выражается четырьмя координатами. Соотнося результаты наблюдений двух обитателей, следует учитывать: часть того, что для одного – пространство, для другого – время, и наоборот. Это обстоятельство легко выразить в математическом уравнении или с помощью подобия, но почти невозможно прийти к нему на интуитивном уровне.

Пространство-время Минковского предполагает некоторую аскетичность, так как тела в нем движутся с постоянной скоростью. С четырехмерной перспективы предметы без ускорения изображаются как точки или как прямые линии. С введением гравитации и ускорения прямые искривляются, они ведут себя подобно двум параллельным линиям, проведенным на поверхности сферы. Прямая линия из двумерного мира, огибая шар, превращается в дугу, а прямые траектории из специальной теории относительности превращаются в геодезические кривые с ускорением в мире общей теории относительности.

На искривленной поверхности мы можем описать окрестность точки с помощью касательной плоскости. Этот же способ поможет нам, хотя и на небольших участках, физически описать траекторию тела с ускорением при помощи свободного падения. Приближение будет более или менее точным в зависимости от кривизны пространства (иными словами, в зависимости от ускорения, воздействующего на тело).