Стивен Вайнберг - Объясняя мир. Истоки современной науки

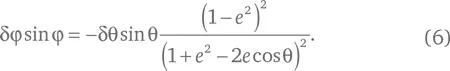
Теперь нам нужна формула, связывающая sin φ и sin θ. Для этого посмотрим на рис. 15 и обратим внимание, что вертикальная координата y точки на линии эллипса выражается как y = r + sin θ, а также y = r − sin φ, и, поделив их, сократив y , получаем:

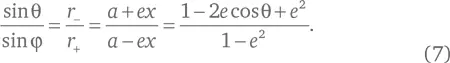
Совмещая уравнения (7) и (6), имеем:

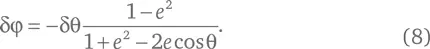
Итак, какова же площадь, описываемая радиус-вектором планеты, проведенным от Солнца, когда угол θ изменяется на δθ? Измеряя углы в градусах, мы можем сказать, что это площадь равнобедренного треугольника, две равные стороны которого имеют длину r +, а третья – маленькая часть дуги общей длиной 2 πr +окружности радиусом r +, равная 2 πr +× δθ/360°. Она равна

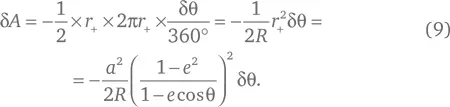
В этой формуле поставлен минус, поскольку мы хотим, чтобы величина δ A росла, если увеличивается угол φ; но если вспомнить, как мы определили эти углы, φ будет расти в том случае, если уменьшается θ, поэтому δφ больше нуля, когда δθ меньше нуля. Поэтому уравнение (8) можно переписать в виде:

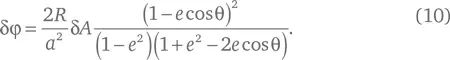
Принимая, что δ A и δφ – описываемая первым радиус-вектором площадь и угол поворота второго радиус-вектора за ничтожно малый промежуток времени δ t , и поделив обе части уравнения (10) на δ t , найдем соответствие между описываемыми площадями и углами в виде равенства

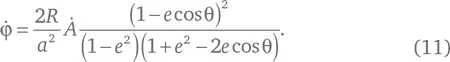
Нами получено точное равенство. Но теперь посмотрим, как оно себя ведет в том случае, когда e очень мал. Числитель второй дроби в уравнении (11) имеет вид (1 − e cos θ)² = 1 − 2 e cos θ + e ²cos²θ, так что слагаемые нулевого и первого порядка в числителе и знаменателе дроби одни и те же, и вся разница между числителем и знаменателем заключается в коэффициентах членов, пропорциональных e ². И значит, уравнение (11) полностью соответствует искомому нами с самого начала равенству (1). Для большей определенности мы можем оставить в уравнении (11) члены порядка e ²:

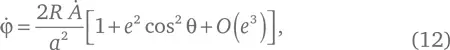
где O ( e ³) обозначает члены, пропорциональные e ³ или более высоким степеням e .

Рассмотрим поставленную вертикально линзу с выпуклой передней стороной и плоской задней – похожие линзы Галилей и Кеплер использовали для изготовления объективов своих телескопов. Из криволинейных поверхностей легче всего полировать сферические, и мы допустим, что форма передней поверхности линзы – сегмент сферы радиусом r . Также в наших рассуждениях будем считать, что линза тонкая, то есть ее максимальная толщина значительно меньше, чем r .

Пусть луч света горизонтально падает на линзу параллельно ее оси и встречается с поверхностью линзы в точке P . В этом случае отрезок от расположенного позади линзы центра кривизны C сферической поверхности до точки P образует с центральной осью линзы угол θ. Линза преломит луч света таким образом, что после того, как он выйдет из ее толщи через заднюю поверхность, он пересечет ось под другим углом, который мы обозначим φ. Точку его пересечения с осью симметрии линзы обозначим F (см. рис. 16а). Нам требуется рассчитать расстояние f , которое отделяет эту точку от линзы, и доказать, что оно не зависит от θ, за счет чего все параллельные лучи, падающие на линзу горизонтально, пересекают ее центральную ось в точке F . Говорят, что в этом случае лучи фокусируются линзой в точке F , а расстояние f от нее до линзы называется фокусным расстоянием.

Для начала обратим внимание, что длина дуги вдоль передней поверхности линзы от оси линзы до точки P есть доля θ/360° от полной длины окружности, образующей сферы 2 πr . С другой стороны, та же самая дуга составляет φ/360° от полной длины окружности радиусом f , которая равна 2 πf . Будем считать, что эти две дуги одинаковые, и приравняем их:

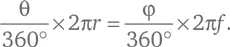
Теперь, сокращая в правой и левой частях 360° и 2 π , получаем пропорцию:

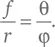
Значит, чтобы рассчитать фокусное расстояние линзы, нужно найти отношение φ к θ.

Для этого нужно обратить внимание, что именно происходит с лучом света внутри линзы (см. рис. 16б). Отрезок от центра кривизны C до точки P , в которой горизонтальный луч падает на линзу, перпендикулярен выпуклой сферической поверхности линзы в точке P , поэтому угол между этим перпендикуляром и лучом (то есть угол падения луча) равен θ. Как известно еще со времен Клавдия Птолемея, если угол θ достаточно мал (а для тонкой линзы так и есть), то угол α между направлением луча в толще стекла и тем же перпендикуляром (то есть угол преломления луча) пропорционален углу падения:

где n > 1 – постоянная величина, называемая коэффициентом преломления, которая зависит от свойств стекла и окружающей среды – чаще всего это воздух (Ферма показал, что n равно скорости света в воздухе, деленной на скорость света в стекле, но нам это знать необязательно). В таком случае угол β между лучом света в толще стекла и осью линзы равняется:

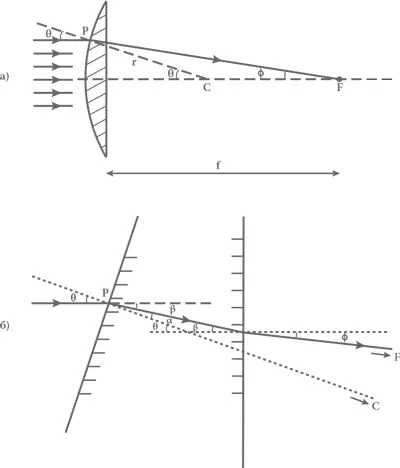
Рис. 16. Фокусное расстояние линзы:а) определение фокусного расстояния. Горизонтальная штриховая прямая – оптическая ось линзы. Линии со стрелками обозначают направление лучей света, падающих на линзу параллельно ее оси. Мы рассматриваем один луч, который падает на линзу в точке P , в которой он образует малый угол θ, с перпендикулярной поверхности прямой, проходящей через точку P и центр кривизны C поверхности линзы. Этот луч преломляется линзой, выходя из нее идет под углом φ к оси линзы и пересекает ее в точке F , находящейся на расстоянии f от линзы. Это расстояние и называется фокусным. Поскольку θ пропорционален φ, все горизонтальные лучи собираются линзой в этой точке; б) вычисление фокусного расстояния. Здесь показан маленький фрагмент линзы, где наклонная сплошная линия со штриховкой слева обозначает небольшой сегмент передней выпуклой поверхности линзы. Сплошная линия со стрелкой отмечает путь луча, преломляемого линзой, который входит в ее толщу в точке P под небольшим углом θ к перпендикуляру к поверхности в этой точке. Этот перпендикуляр показан на чертеже как наклонная пунктирная линия – часть прямой, проходящей через точку P и центр C кривизны поверхности линзы, который не показан, потому что находится за границей этого чертежа. Входя внутрь линзы, луч преломляется и образует угол α с этим перпендикуляром, а покидая ее, преломляется снова, образуя угол φ с перпендикуляром к плоской задней поверхности линзы. Этот второй перпендикуляр показан на чертеже как пунктирная прямая, параллельная оптической оси линзы.