Шон Кэрролл - Частица на краю Вселенной. Как охота на бозон Хиггса ведет нас к границам нового мира

Первая перспективная теория слабых взаимодействий была предложена Энрико Ферми в 1934 году. Ферми воспользовался идеей нейтрино, незадолго до этого выдвинутой Вольфгангом Паули для построения модели нейтронного распада, протекающего – как теперь мы бы сказали – по каналам слабых взаимодействий. Как мы увидели в главе 7, расчет Ферми, кроме того, был одним из первых успешных расчетов в рамках квантовой теории поля.

Теория Ферми хорошо описывает данные, но только если не требовать от нее слишком многого. Многие расчеты в квантовой теории поля строятся по такой схеме: сначала находится приблизительный ответ, а затем постепенно включаются вклады от более сложных диаграмм Фейнмана, и ответ шаг за шагом уточняется. В теории Ферми начальное приближение дает очень хороший ответ, но следующая аппроксимация (которая должна быть небольшой поправкой) оказывается бесконечной. Эта неприятность называется проблемой расходимости, тут сидит большая проблема, которая будет довлеть над физикой элементарных частиц на протяжении всего XX века. Бесконечность, конечно, не может быть правильным ответом, поэтому она служит указанием на то, что ваша теория где-то не верна. Теория должна соответствовать экспериментальным данным, но она также должна быть правильной и в математическом смысле.

Проблема расходимости возникает не только в слабых взаимодействиях, от нее пострадал и электромагнетизм – по идее одна из самых простых и легких для понимания квантовых теорий поля из всех существующих на данный момент. Оказывается, однако, что бесконечности можно приручать. Подобная процедура называется «перенормировкой», и за ее изобретение Фейнман, Швингер и Томонага получили Нобелевскую премию.

Некоторые теории поля перенормируемы (и для них есть четко определенные математические методики получения конечных ответов), а некоторые – нет. В современной квантовой теории поля даже если теория не перенормируема, мы не отбрасываем ее. Мы просто считаем, что это приближение справедливо в лучшем случае только при очень низких энергиях, а при более высоких энергиях для устранения бесконечности нужно найти какие-то новые физические законы. В течение долгого времени, однако, неперенормируемость воспринималась как указание на то, что теория просто неправильна. Теория слабых взаимодействий Ферми оказалась неперенормируемой – как только мы пытаемся выжать из нее слишком много, она дает бесконечный ответ, и нет никакого способа избавиться от этого, кроме как придумать лучшую теорию.

Джулиан Швингер, который заинтересовался идеей Янга-Миллса о том, что более сложные симметрии могут приводить к появлению калибровочных полей, порождающих силы природы, попытался применить эту идею к слабым взаимодействиям. Конечно, тут же возникла большая проблема: бозоны Янга-Миллса не имеют массы, а это подразумевает силу, действующую на больших расстояниях, в то время как слабое взаимодействие явно ограничено очень малыми расстояниями. Швингер просто отложил эту проблему на время в сторону, начал с модели Янга-Миллса и в ней искусственно положил массу двух бозонов – переносчиков сил – ненулевой. Это было первое упоминание бозонов, которые мы теперь называем W +– и W −-бозонами. (По крайней мере, одно из первых. По словам Леона Ледермана, «в более поздних версиях теории Ферми, в первую очередь у Швингера, были введены тяжелые W +– и W −-бозоны в качестве носителей слабого взаимодействия. Похожую идею использовали и некоторые другие теоретики. Попробую перечислить: Ли, Янг, Гелл-Манн… Я не люблю хвалить конкретных теоретиков, поскольку 99 % остальных расстроятся».)

Бозоны Янга-Миллса были безмассовыми в первую очередь из-за симметрии, на которой строилась теория. Когда Швингер наделил бозоны массой, это означало, что симметрия нарушилась, но в данном случае это было явное (или жесткое) нарушение, а не «спонтанное », при котором симметрия скрыта неким полем, имевшим отличное от нуля значение в пустом пространстве (и к тому времени еще не открытое). В теории Швингера симметрия нарушалась не из-за поля, а потому что он ей так велел. Как вы можете догадаться, это искусственное предположение уменьшало доверие к модели. Прежде всего, перенормируемость электромагнетизма в решающей степени зависит от симметрии, лежащей в основе теории, и пренебрежение этой симметрией делает модель Швингера неперенормируемой. В конце концов, но много лет спустя, стало ясно, что теория массивных калибровочных бозонов станет перенормируемой тогда и если их массы приобретаются в результате спонтанного нарушения симметрии.

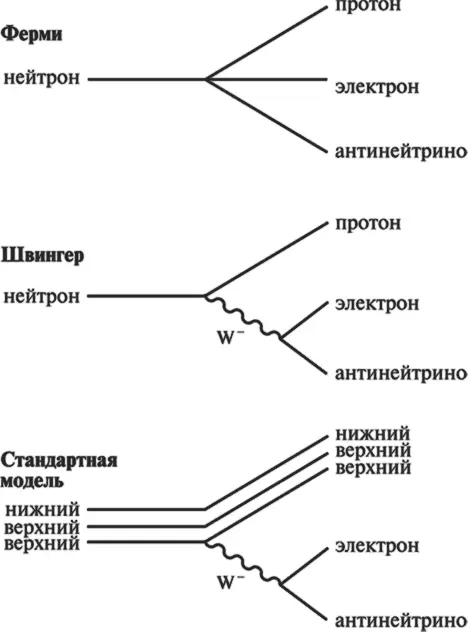
Пример изменения представлений о распаде нейтрона. В теории Ферми нейтрон распадается непосредственно на протон, электрон и антинейтрино. Швингер предположил, что нейтрон испускает заряженный W-бозон, который затем распадается на электрон и антинейтрино. Он был прав, но сейчас мы знаем, что нейтрон состоит из трех кварков, один из которых меняет вид с нижнего на верхний, испуская при этом W-бозон.

Тем не менее Швингер продолжал искать способы обойти эти трудности, и не только из упрямства. Одно из свойств гения в том, что он чувствует, какие идеи стоит развивать, даже если они не во всех отношениях соответствуют действительности. Важным следствием модели Швингера было то, что она предсказала три калибровочных бозона: два заряженных массивных W-бозона, и один нейтральный калибровочный бозон, которому было разрешено остаться без массы. Все мы, конечно, отлично знакомы с нейтральным безмассовым калибровочным бозоном: это фотон. Швингер был воодушевлен тем, что его подход дал надежду объединить электромагнетизм со слабыми взаимодействиями, что явилось бы важным шагом вперед в физике. Это, наверное, и давало ему силы и дальше совершенствовать свою модель, несмотря на кучу проблем.

Однако довольно скоро он бросил заниматься своей моделью. Статья Швингера была опубликована в 1957 году, и в том же году обнаружилось, что слабые взаимодействия нарушают четность. Вспомним, как в главе 8 мы говорили (и еще скажем в Приложении 1), что частицы являются либо левшами, либо правшами в зависимости от того, в каком направлении они вращаются. Нарушение четности подразумевает, что слабые силы воздействуют только на частицы-левши. Можно придумать симметрии Янга-Миллса, в которых задействованы лишь вращающиеся против часовой стрелки частицы, но мы знаем, что электромагнитные взаимодействия не нарушают четности – они обращаются и с левшами и с правшами одинаково. Это открытие, казалось, поставило крест на надежде Швингера объединить слабые и электромагнитные взаимодействия.