Леонард Сасскинд - Космический ландшафт. Теория струн и иллюзия разумного замысла Вселенной

S-матрица – это просто таблица квантово-механических вероятностей. Вы имеете входные данные, а S-матрица сообщает вам вероятности того, что вы можете получить на выходе. Таблица вероятностей зависит от направлений и энергий входящих и выходящих из чёрного ящика частиц, и, согласно превалирующей идеологии середины 1960-х годов, теория элементарных частиц должна быть строго ограничена изучением зависимости S-матрицы от этих переменных. Всё остальное было запрещено. Идеологи решили, что они лучше знают, как лучше для науки, и превратились в стражей научного пуризма. Теория S-матрицы была здоровым напоминанием о том, что физика является эмпирической наукой, но, как и в случае с бихевиористами, философия S-матрицы завела их слишком далеко. По мне, это всё походило на засовывание удивительного цветного мира в серый унылый стерилизатор бухгалтерских таблиц. И я взбунтовался. Но у меня не было подходящей для бунта теории.

В 1968 году молодой итальянский физик Габриэле Венециано жил и работал в Израиле в институте Вейцмана. Он не был идеологически подкован в вопросах теории S-матрицы, но его занимала одна имеющая отношение к S-матрице математическая задача. Существовали определённые технические требования, которым должна удовлетворять S-матрица, но никто до того времени не мог написать ни одного удовлетворяющего этим требованиям математического выражения. Венециано пытался найти хотя бы одно. Его попытка завершилась блестящим успехом. Он получил чрезвычайно аккуратный результат, известный сегодня как «амплитуда Венециано». Но это не было изображением внутреннего строения каких-то частиц или визуализацией процессов столкновения. Амплитуда Венециано была красивым математическим выражением – элегантной математической таблицей вероятностей.

Процесс открытия теории струн, который в определённом смысле все ещё продолжается, изобиловал поворотами судьбы, предательствами фортуны и интуитивными озарениями. Моё собственное участие в нём началось где-то в конце 1968 или в начале 1969 года. Я начал уставать от проблем элементарных частиц; особенно досаждали мне адроны, концепция которых, казалось, мало что может предложить в плане новых глубоких принципов. Я нашёл метод S-матрицы скучным и начинал подумывать о том, чтобы заняться соединением квантовой механики и гравитации. Соединение общей теории относительности с принципами квантовой механики казалось гораздо более интересной задачей, несмотря на то что все имевшиеся экспериментальные данные касались исключительно адронов. Но как раз в это время меня посетил в Нью-Йорке мой израильский друг Гектор Рубинштейн, который был чрезвычайно воодушевлён работой Венециано.

Сначала я не особо заинтересовался. Адроны были тем, о чём я хотел забыть, но из вежливости я согласился выслушать Гектора.

Гектор был настолько возбуждён, объясняя мне идеи итальянца, что я не вполне улавливал детали. Насколько я мог понять, Венециано придумал формулу для описания того, что произойдёт при столкновении двух адронов. Наконец, Гектор записал уравнение Венециано на доске в моем офисе. Это был финальный аккорд. Уравнение оказалось чрезвычайно простым и имело некоторые особенности, показавшиеся мне подозрительно знакомыми. Я, помню, спросил Гектора, не представляет ли это уравнение описание какой-то очень простой квантово-механической системы, потому что оно выглядело так, будто бы имело отношение к гармоническим осцилляторам. Гектор не знал, какая физическая картина могла бы стоять за этим уравнением, поэтому я просто записал его на листке бумаги, чтобы не забыть.

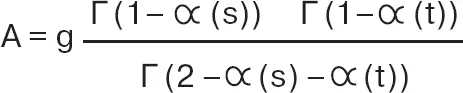
Я был достаточно заинтригован, чтобы отложить размышления о квантовой гравитации и дать адронам ещё один шанс. Как оказалось, мне не суждено было вернуться к гравитации в течение последующих лет. Я несколько месяцев обдумывал это уравнение, прежде чем увидел то, что стояло за ним в действительности.

Термин гармонический осциллятор применяется физиками ко всему, что способно вибрировать, дрожать, колебаться или вообще совершать периодические движения туда-сюда. Ребёнок, качающийся на качелях, и грузик, колеблющийся на пружине, являются примерами типичных гармонических осцилляторов. Вибрирующая скрипичная струна или даже воздух, через который проходит звуковая волна, – это тоже гармонические осцилляторы. Если колеблющаяся система очень мала, например если это атом или молекула, то её поведение определяется законами квантовой механики, и энергия такого осциллятора может изменяться только дискретными порциями. Я упомянул гармонический осциллятор в беседе с Гектором, потому что уравнение Венециано напомнило мне о математических свойствах квантово-механического гармонического осциллятора. Я представил себе адрон в виде двух грузиков, соединённых пружиной, совершающих гармонические колебания, сближаясь и удаляясь. Я играл с запретным плодом, пытаясь изобразить внутреннее устройство элементарной частицы, и отдавал себе в этом отчёт.

Танталовы муки, которые я испытывал от ощущения близости ответа и невозможности его ухватить, сводили меня с ума. Я испробовал все варианты квантово-механических осцилляторов, пытаясь подобрать такой, который вписался бы в уравнение Венециано. Мне удалось написать уравнения, очень похожие на уравнения Венециано, описывающие разные варианты моделей грузиков на пружинках, но все они не годились. В течение этого периода я потратил много часов собственного времени, работая на чердаке своего дома. Возвращаясь оттуда усталым и раздражительным, я ругался с женой и игнорировал детей. Мне не удавалось выкинуть это уравнение из головы даже во время обеда. И вдруг, в один из вечеров, без всякой уважительной причины на меня на чердаке снизошло озарение. Я не знаю, что вызвало к жизни эту мысль: ещё минуту назад я представлял себе пружину и вдруг увидел вместо неё эластичную струну, натянутую между двумя кварками и имеющую много различных мод колебаний. В одно мгновение я понял, что весь трюк состоит в том, чтобы заменить математическую пружину непрерывной натянутой струной. На самом деле слово струна тогда не пришло мне на ум. Я подумал о резиновом кольце . Если разрезать резиновое кольцо, оно превратится в резинку с двумя свободными концами. На каждый из концов я мысленно поместил по кварку, точнее, кварк на один конец и анти-кварк на другой.

Я быстро сделал несколько расчётов в своей записной книжке для проверки идеи, хотя уже знал, что это будет работать. Это было потрясающе просто. Уравнение Венециано для S-матрицы оказалось точным описанием столкновения двух резинок. Почему эта мысль раньше не приходила мне в голову?