Леонард Сасскинд - Космический ландшафт. Теория струн и иллюзия разумного замысла Вселенной
- Название:Космический ландшафт. Теория струн и иллюзия разумного замысла Вселенной
- Автор:
- Жанр:
- Издательство:Издательство «Питер»046ebc0b-b024-102a-94d5-07de47c81719
- Год:2015
- Город:Санкт-Петербург
- ISBN:978-5-496-01166-2
- Рейтинг:
- Избранное:Добавить в избранное
-
Отзывы:
-
Ваша оценка:
Леонард Сасскинд - Космический ландшафт. Теория струн и иллюзия разумного замысла Вселенной краткое содержание
Леонард Сасскинд, известный американский физик и один из создателей теории струн, в свое время предложил революционную концепцию понимания Вселенной и места человека в ней. Своими исследованиями Сасскинд вдохновил целую плеяду современных физиков, которые поверили, что эта теория сможет однозначно предсказать свойства нашей Вселенной. Теперь же в своей первой книге для широкого круга читателей Сасскинд уточняет и переосмысляет свои взгляды, утверждая, что данная идея отнюдь не универсальна и ей придется уступить место гораздо более широкому понятию гигантского «космического ландшафта».
Исследования начала XXI века позволили науке подняться на новую ступень в познании мира, утверждает Сасскинд. И эта увлекательная книга, переносящая читателя на передовую сражений в современной физике, – яркое тому подтверждение.
Космический ландшафт. Теория струн и иллюзия разумного замысла Вселенной - читать онлайн бесплатно ознакомительный отрывок
Интервал:
Закладка:
Но примерно в начале 1970-х вдохновлённые первыми успехами теории струн теоретики начали играться с новыми математическими идеями, согласно которым фермионы и бозоны на самом деле не настолько различны. Одна из идей состояла в том, что все частицы образуют идеальные пары идентичных близнецов, одинаковых во всех отношениях, за исключением того, что один из них является фермионом, а другой – бозоном. Это была совершенно дикая гипотеза. Её справедливость для реального мира означала бы, что физики умудрились каким-то образом потерять половину всех элементарных частиц, не сумев обнаружить их в своих лабораториях. Например, согласно этой гипотезе, должна существовать частица с точно такой же массой, зарядом и прочими свойствами, как у электрона, только являющаяся не фермионом, а бозоном. Как можно было не заметить такую частицу на ускорителях Стэнфорда или ЦЕРНа? Суперсимметрия предполагает существование у фотона безмассового нейтрального близнеца-фермиона, а также близнецов-бозонов у электронов и кварков. То есть гипотеза предсказывала целый мир таинственно пропавших без вести «противоположностей». На самом деле вся эта работа была лишь математической игрой, чисто теоретическими исследованиями нового вида симметрии – мира, которого нет, но который мог бы существовать.
Идентичных частиц-близнецов не существует. Физики не лажанулись и не проворонили целый параллельный мир. Какой же интерес в таком случае представляет эта математическая спекуляция и почему этот интерес вдруг усилился за последние 30 лет? Физиков всегда интересовали всевозможные математические симметрии, даже если единственный разумный вопрос, который можно было при этом задать: «Почему этой симметрии нет в природе?» Но и реальный мир, и его физическое описание полны разнообразных симметрий. Симметрия является одним из наиболее дальнобойных и мощных орудий в арсенале теоретической физики. Она пронизывает все разделы современной физики, и особенно те, которые связаны с квантовой механикой. Во многих случаях тип симметрии – это всё, что мы знаем о физической системе, но анализ симметрии является настолько мощным методом, что зачастую сообщает нам почти всё, что мы хотим знать. Симметрии нередко являются тем садом, в котором физики находят эстетическое удовлетворение от своих теорий. Но что такое симметрии?
Начнём со снежинки. Любой ребёнок знает, что не существует двух одинаковых снежинок, но вместе с тем все они имеют общую особенность, а именно симметрию. Симметрия снежинки сразу бросается в глаза. Если вы возьмёте снежинку и повернёте её на произвольный угол, то она будет выглядеть отличной от своего первоначального вида – повёрнутой. Но если повернуть снежинку ровно на 60°, то она совпадёт сама с собой. Физик мог бы сказать, что поворот снежинки на 60° является симметрией.
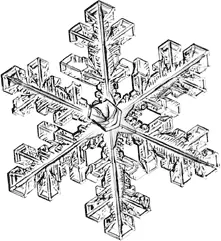
Симметрии связаны с операциями или преобразованиями, которые можно выполнять над системой, не влияя на результат эксперимента. В случае снежинки такой операцией является поворот на 60°. Вот ещё один пример: предположим, что мы ставим эксперимент, имеющий целью измерение ускорения свободного падения на поверхности Земли. Простейшим вариантом было бы уронить камень с известной высоты и измерить время его падения. Ответ: около 10 метров в секунду за секунду. Обратите внимание, что я не беспокоюсь о том, чтобы сообщить вам, где я уронил камень: в Калифорнии или в Калькутте. В очень хорошем приближении ответ будет одним и тем же в любом месте на поверхности Земли: результат эксперимента не изменится, если вы переместитесь со всем экспериментальным оборудованием с одного места земной поверхности на другое. На физическом жаргоне сдвиг или перемещение чего-либо из одной точки в другую называется трансляцией . Поэтому о гравитационном поле Земли мы можем сказать, что оно обладает «трансляционной симметрией». Конечно, некоторые побочные эффекты могут внести возмущения в результаты нашего эксперимента и испортить симметрию. Например, проведя эксперимент над очень большими и массивными месторождениями полезных ископаемых, мы получим немного большее значение, чем в других местах. В этом случае мы бы сказали, что симметрия является только приблизительной. Приблизительную симметрию называют также нарушенной симметрией . Наличие отдельных залежей тяжёлых минералов «нарушает трансляционную симметрию».
Может ли симметрия снежинки быть нарушенной? Без сомнения, некоторые снежинки несовершенны. Если снежинка формируется в неидеальных условиях, то одна её сторона может отличаться от другой. Она всё ещё будет иметь форму, близкую к шестиугольной, но этот шестиугольник будет несовершенным, то есть его симметрия будет нарушена.
В космическом пространстве, вдали от каких-либо возмущающих влияний, мы могли бы измерить гравитационную силу между двумя массами и получить ньютоновский закон всемирного тяготения. Независимо от того, где проведён эксперимент, мы, по идее, должны получить один и тот же ответ. Таким образом, ньютоновский закон всемирного тяготения обладает трансляционной инвариантностью .
Для измерения силы притяжения между двумя объектами необходимо расположить их на некотором расстоянии друг друга. Например, мы можем расположить два объекта так, что соединяющая их прямая будет параллельна оси x в некоторой заданной системе координат. С равным успехом мы можем расположить объекты на прямой, параллельной оси y . Будет ли измеряемая нами сила притяжения зависеть от направления прямой, соединяющей эти объекты? В принципе, да, но только если законы природы отличаются от тех, которые у нас есть. В природе же закон всемирного тяготения утверждает, что сила притяжения пропорциональна произведению масс и обратно пропорциональна квадрату расстояния между ними и она не зависит от ориентации одного объекта относительно другого. Независимость от направления называется вращательной симметрией . Трансляционная и вращательная симметрии являются важнейшими фундаментальными свойствами мира, в котором мы живём.
Посмотрите в зеркало. Ваше отражение как две капли воды похоже на вас. Зеркальное отражение ваших брюк ничем не отличается от самих брюк. Отражение левой перчатки в точности повторяет левую перчатку.
Стоп. Что-то тут не так. Давайте посмотрим ещё раз внимательно. Зеркальное отражение левой перчатки не во всём идентично левой перчатке. Оно идентично правой перчатке! А зеркальное отражение правой перчатки идентично левой перчатке.
Теперь присмотритесь внимательнее к собственному отражению. Это не вы. Родинка, которая у вас находится на левой щеке, у вашего отражения находится на правой. А если бы вы вскрыли собственную грудную клетку, то обнаружили бы, что сердце у вашего отражения находится не слева, как у всех нормальных людей, а справа. Давайте назовём зеркального человека – 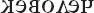 .
.
Интервал:
Закладка:









