Леонард Сасскинд - Космический ландшафт. Теория струн и иллюзия разумного замысла Вселенной

Следующее озарение принесла квантовая механика. Подобно любым другим колебательным движениям движение в направлении компактной y -координаты квантовано. Частица не может двигаться вдоль оси y с произвольным значением проекции импульса на ось y . Оно может принимать только дискретные значения, так же как и в гармоническом осцилляторе или у электрона в атомной теории Бора. А это, в свою очередь, означает, что момент в y -измерении и, соответственно, заряд электрона не могут принимать произвольные значения. Электрический заряд в теории Калуцы квантован, он может выражаться только произведением заряда электрона на целое число. Заряд частицы может в два или в три раза превышать заряд электрона, но не может отличаться от него, например, в 1,88 или в 0,067 раза. И это радует. В реальном мире не обнаружено ни одного объекта, имеющего дробный (в единицах заряда электрона) заряд: все электрически заряженные тела имеют заряд, кратный заряду электрона.

Это потрясающее открытие, тем не менее, так и оставалось не более чем «интересной идеей» на протяжении всей оставшейся жизни Калуцы. Но для нашей книги оно имеет ключевое значение. Теория Калуцы продемонстрировала, как свойства частиц могут возникать из дополнительных пространственных измерений. И действительно, обнаружив, что теория струн требует шести дополнительных измерений, струнные теоретики вспомнили об идеях Калуцы. Достаточно просто свернуть шесть дополнительных измерений надлежащим образом, чтобы движением в них объяснить внутреннюю машинерию элементарных частиц.

Возможности теории струн гораздо богаче, чем теории точечных частиц. Вернёмся к цилиндру и предположим, что по его поверхности движется маленькая замкнутая струна. Начнём с цилиндра, окружность которого достаточно велика, чтобы видеть её невооружённым глазом. Маленькая замкнутая струна может двигаться по нему таким же образом, как и точечная частица: вдоль образующей цилиндра или вокруг его оси. В этом случае движение струны принципиально не отличается от движения точечной частицы. Но есть кое-что, на что струна способна, а точечная частица – нет. Струна может быть обёрнута вокруг цилиндра подобно резиновому кольцу, надетому на картонную трубку. Обёрнутая вокруг цилиндра струна отличается от необёрнутой. Резиновое кольцо можно надеть на цилиндр так, что оно будет оборачивать его дважды, трижды и т. д., пока оно не порвётся. Этот мысленный эксперимент приводит нас к новому свойству струн, которое в принципе отсутствует у точечных частиц, называемому числом кручения . Это число сообщает нам, сколько витков струны намотано на компактное измерение.

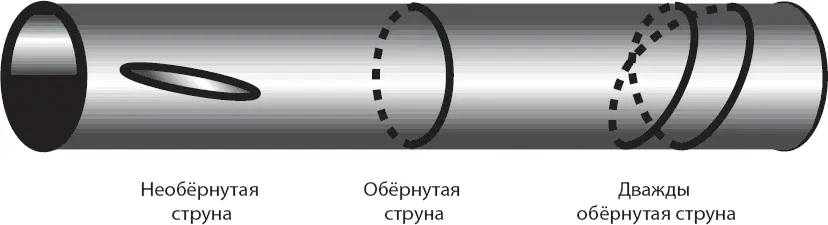
Число кручения является тем свойством частицы, которое невозможно понять, если наш микроскоп недостаточно силён, чтобы разрешать детали, имеющие размеры, сравнимые с размером компактного измерения. Как вы теперь понимаете, дополнительные измерения оказались благословением, а не проклятием для теории струн, поскольку они необходимы для объяснения сложных свойств элементарных частиц.

Двумерный цилиндр изобразить достаточно легко, но я сомневаюсь, чтобы кто-нибудь был в состоянии представить себе девятимерный мир, шесть измерений которого свёрнуты в крошечное шестимерное пространство. Но рисование картинок на листе бумаги или представление моделей в голове не единственный способ оперировать шестимерной геометрией теории струн. Часто геометрия может быть сведена к алгебре точно таким же способом, которым вы в школе описывали различные геометрические фигуры, например окружность или прямую, при помощи уравнений. Тем не менее даже самые мощные математические методы часто пасуют перед шестимерной геометрией.

Например, число возможных путей, по которым может катиться шарик по поверхности в шестимерной геометрии теории струн, исчисляется миллионами. Я не стану описывать эти пространства, а только сообщу, что они носят наименование пространств или многообразий Калаби – Яу в честь двух математиков, потративших массу усилий на их изучение. Я не знаю, с чего вдруг математики заинтересовались этими многообразиями, но они оказались чрезвычайно полезными для струнных теоретиков. К счастью, единственное, что следует знать про эти пространства для понимания дальнейшего материала, – это то, что они представляют собой очень сложные конструкции с сотнями дыр наподобие дыр от бублика и прочими особенностями.

Вернёмся к двумерному цилиндру. Длина окружности цилиндра характеризует так называемый масштаб компактификации . Для картонного цилиндра этот масштаб составляет несколько сантиметров, для теории струн он должен быть порядка нескольких планковских длин. Если вы решите, что этот масштаб слишком мал, чтобы иметь какое-то значение для тех вещей, которыми мы обычно занимаемся, то сильно ошибётесь. Хотя мы и не в состоянии наблюдать или измерять столь малые вещи, они имеют определяющее значение для обычной физики. Масштаб компактификации в теории Калуцы определяет величину электрического заряда частицы, например электрона. Другими словами, масштаб компактификации определяет величину различных констант, которые присутствуют в обычных законах природы. При изменении размера нашего цилиндра изменяются и Законы Физики. Если изменить величины скалярных полей, о которых я рассказывал в главе 1, Законы Физики тоже изменятся. Есть ли здесь какая-то связь? Безусловно! И сейчас мы о ней поговорим.

Чтобы задать свойства цилиндра, достаточно задать величину масштаба компактификации, но для других фигур этого недостаточно. Например, для описания тора необходимо задать три параметра. Попробуем себе это представить. Первым параметром является внешний размер тора. Тор можно увеличить или уменьшить, не изменяя его формы. Кроме того, тор может быть «тонким», как обруч, или «толстым», как пышка. Параметр, характеризующий толщину тора, называется аспектным отношением . Аспектное отношение определяется как отношение большого радиуса тора (определяющего внешний размер) к радиусу трубки. Для тонкого тора аспектное отношение велико, для толстого тора оно стремится к единице. Существует ещё один параметр, который достаточно трудно изобразить на рисунке. Представьте себе, что мы разрезали тор, так, чтобы получился цилиндр, после этого, взявшись за один из концов цилиндра, начали его закручивать относительно оси цилиндра, а потом снова соединили цилиндр в тор по линии разреза. Угол, на который мы закрутили цилиндр, и есть третий параметр. Я попытался это изобразить на третьей картинке.