Сергей Зимов - Азбука рисунков природы

Во многих случаях и для величины пороговой функции необходимо задавать направление. Например, прочность на разрыв у многих материалов в различных направлениях может сильно различаться (пример — деревянная доска трескается вдоль, а торец бревна — по радиусу или окружности). Соответственно трещины в таких материалах будут возникать не вкрест направлению максимальных растягивающих напряжений, а в том направлении, где в первую очередь напряжения достигнут величины прочности, наблюдаемой в этом же направлении.

У линейных элементов может быть специфична и разгрузка потенциальной функции. Вблизи элемента величина потенциала может разгружаться во всех направлениях, а может преимущественно или (лишь) в каком-то одном. Все это значительно усложняет анализ, формализацию и графическое выражение механизмов формирования рисунка. Тем не менее попытаемся это сделать. Оговорим, что составляющую потенциала для какого-то направления в точке пространства будем считать мерой возможности появления в данной точке структурного линейного элемента, ориентированного в этом направлении. В ряде случаев потенциал можно задать как вероятность появления в этом направлении элемента. Отметим, что направление, в котором наш потенциал максимален, может не соответствовать направлению реальных параметров. Так, например, трещины возникают в направлении, перпендикулярном направлению максимальных растягивающих напряжений.

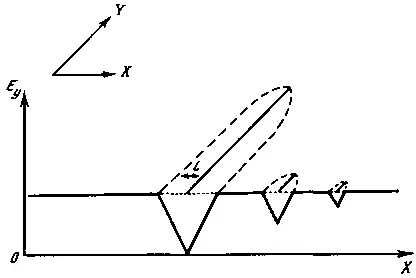
Рис. 55

Конкретные примеры мы пока рассматривать не будем, а сразу начнем с абстрактных схем. Будем задавать различные варианты пороговой и потенциальной функций, их динамики и условий разгрузки, получая в итоге различные рисунки.

Начнем наши примеры со структур, возникающих на плоскости xy в резко анизотропном потенциальном поле. Примем, что потенциал везде ориентирован в направлении y , во всех других же направлениях потенциал равен нулю. Пороговую функцию при этом зададим скалярной величиной; примем, что во всем рассматриваемом пространстве она одинакова. При этих условиях структурные элементы будут возникать там, где величина потенциала достигнет величины пороговой функции. Элементы при этом будут всегда прямыми линиями, ориентированными вдоль направления y . Примем, что на линии элемента разгрузка потенциала полная, ширина зоны разгрузки вокруг линейного элемента конечна и не превышает 2l , при этом величина разгрузки при удалении от элемента изменяется по линейному закону (рис. 55). Примем, что в вершине структурного элемента (у конца линии) ширина зоны разгрузки и ее «глубина» равны нулю и лишь на каком-то удалении от конца, допустим на расстоянии порядка 2l , она достигает конечной ширины и «глубины» — полностью разгружает потенциал (см. рис. 55).

В вершине структурного элемента возможно увеличение значений потенциала или снижение значений пороговой функции — «ослабление прочности», «концентрация напряжений». Из-за этого элемент (линия) может «по инерции» проникать в область, где E y< P . Этот вариант рассмотрим позже, а пока примем, что вершина структурного элемента не может проникать в область пространства, где E y< P .

Рассмотрим особенности формирования рисунка в пределах плоскости, ограниченной прямоугольником с вершинами А, В, С, D. Примем, что его стороны AD и ВС не оказывают влияния на потенциальную функцию, а стороны АВ и CD разгружают ее, как будто они являются структурными элементами. Пусть в пределах выделенного контура величина потенциальной функции будет везде одинакова.

Начнем наращивать потенциал. Его рельеф параллелен пороговому рельефу, поэтому условие E y= P возникнет одновременно по всему контуру. Тогда первый структурный элемент (линия) может возникнуть в любом месте. Допустим, что структурные элементы развиваются моментально, тогда элемент быстро пересечет весь контур вдоль себя и в полосе шириной 2l разгрузит потенциал. Новый элемент образоваться здесь уже не сможет. За пределами же зоны разгрузки первого элемента в случайных местах будут возникать новые элементы. В итоге возникнет структура, состоящая из параллельных линий, расстояние между которыми изменяется от l до 2l (рис. 56, а). Если продолжать наращивание потенциала, то посередине между линиями первой генерации, в первую очередь в наиболее широких полосах, будут возникать линии второй генерации (рис. 56, б) и т. д. Во всех последующих рисунках в правом верхнем углу мы графически будем изображать условия задачи. Прямоугольник — это «карта» рельефа максимальных значений первоначально заданной потенциальной функции. Рельеф будет показан изолиниями и берг-штрихами, показывающими уклон. Если на карте нет изолиний, значит, рельеф горизонтальный. Рядом мы будем изображать индикатрису потенциала, показывающую относительные значения потенциала в координатах рисунка.

Теперь предположим, что элементы развиваются медленно. Тогда по всему полю в случайных местах, определяемых микрошероховатостью, будут возникать короткие растущие линии (штрихи). Пока они короткие (меньше 2l ), их окружает узкая зона разгрузки, поэтому новые элементы могут возникать вблизи с предыдущим. Появление новых элементов и удлинение первоначальных приведет к тому, что вся поверхность перекроется зонами их разгрузки и развитие структуры остановится (рис. 57, а). Если после этого продолжать наращивать значения потенциала, то сразу же начнется удлинение элементов — они будут взаимопроникать в зону разгрузки других, встречных элементов. Возникнут условия конкуренции. Если встречаются два коротких элемента (меньше 2l ) разной длины, то у более длинного зона разгрузки глубже, поэтому он будет проникать в зону разгрузки короткого элемента быстрее, чем короткий в его зону разгрузки. В итоге за счет преимущественного развития наиболее длинных элементов структура, изображенная на рис. 57, а, трансформируется в структуру, подобную приведенной на рис. 57, б. Если при соблюдении условия конечности максимальной ширины зоны разгрузки и дальше продолжать наращивание потенциала, то в итоге можно добиться того, что все элементы пересекут массив. После этого наращивание потенциала приведет к возникновению элементов второй генерации. Если же элементы могут постоянно углубляться и расширять зону разгрузки, то в условиях конкуренции мелкие элементы могут вырождаться.

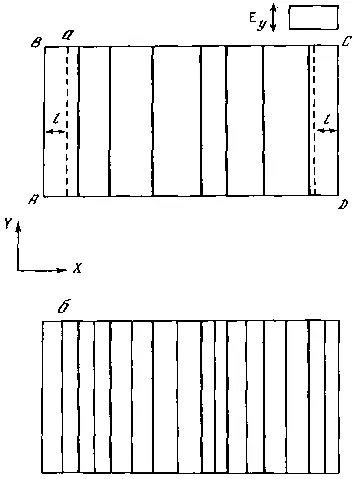
Рис. 56

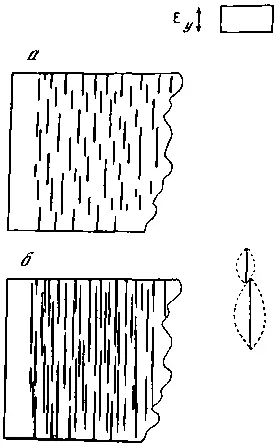
Рис. 57