Сергей Зимов - Азбука рисунков природы

Если принять, что элементы развиваются медленно, а в их вершинах значительной концентрации потенциала не происходит, то первоначально возникнет такая же структура, как изображенная на рис. 57, а. Последующие варианты ее развития при наращивании потенциала будут определяться соотношением E y/E x. Если оно небольшое, то возникнет структура, как на рис. 73. если же это соотношение больше, то к тому моменту, когда выполнится условие E y= P , элементы первой генерации глубоко зайдут в зоны разгрузки друг друга.

Зададим другую форму потенциального рельефа. Пусть он полого наклонен в сторону CD, гребень его максимума располагается на линии разгрузки стороны АВ. На этом гребне и возникнет первый элемент. Примем, что элементы развиваются моментально. Тогда при наращивании потенциала следующий элемент образуется на расстоянии l от первого. Если отношение E y/E xнебольшое, то, еще до того как образуется третий элемент, полоса между этими двумя элементами разобьется поперечными, которые будут удалены один от другого на расстояние от l до 2l . Дальнейшее наращивание значений потенциальной функции приведет к образованию структуры, изображенной на рис. 74, а. Отметим, что в ее левой части могут появиться элементы высших генераций. Если же отношение E y/E xбольшое, то полосы между элементами, ориентированными в направлении y, будут вначале разбиваться элементами более высоких генераций этого же направления, и лишь затем появятся поперечные элементы (рис. 74, б). У этих структур в направлении смещения «границы» элементы строго упорядочены. На рис. 71—74 видно, что по степени вытянутости прямоугольных ячеек можно оценить величину отношения E y/E x.

Изменим наклон потенциального рельефа в сторону ВС, тогда максимум потенциала расположится на границе зоны разгрузки линии AD. При выполнении условия E y= P здесь в случайных местах будут возникать элементы, ориентированные в направлении y. В зависимости от степени концентрации потенциала в вершинах элементов, скорости их развития и наклона потенциального рельефа может возникнуть структура, близкая структурам, изображенным на рис. 59. Как только потенциал возрастет настолько, что выполнится условие E y= P , а произойдет это на границе разгрузки линии AD, то по этому гребню продольные полосы будут разбиты поперечными. Дальнейшее наращивание потенциала вызовет заложение на расстояние l от этой линии новой серии поперечных. В итоге образуется структура, подобная изображенной на рис. 75. В направлении смещающейся границы расстояние между элементами здесь строго выдержано.

Зададим наклон потенциальной поверхности к точке С. Ее максимум (E y) при этом будет расположен на стороне AD на расстоянии l от стороны АВ (на границе разгрузки стороны АВ). Здесь при наращивании потенциала произойдет заложение элемента, ориентированного в направлении y. Следующий элемент возникнет на линии AD на краю зоны разгрузки первого и т. д. Если элемент не может проникнуть глубоко в зону Е < Р, то его зона разгрузки будет узкой и расстояние между элементами будет меньше l и будет зависеть от угла наклона фронта структурообразования. В какой-то момент выполнится условие E y= P . Произойдет это на линии АВ на границе разгрузки стороны AD. Здесь образуется первый элемент, ориентированный вдоль оси x . Следующие поперечные элементы образуются рядом также на линии АВ и «в другой стороне» на продолжении первого (рис. 76). В итоговой структуре из-за того, что граница смещается относительно обеих осей координат, элементы строго упорядочены и в направлении y , и x . Вблизи точки А в этой структуре могут появиться элементы высших генераций.

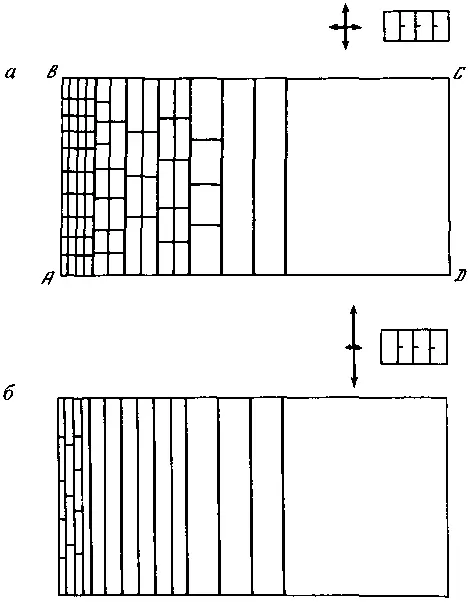
Рис. 74

Сохраним условие наклона потенциального рельефа от точки А к точке С, но развернем массив относительно осей координат. В этом случае образующиеся элементы не будут параллельны сторонам прямоугольного контура. Структура, возникшая в этих условиях при наращивании потенциала, показана на рис. 77.

Теперь охарактеризуем некоторые тетрагональные сетчатые структуры, возникающие в пределах пространства, ограниченного кругом. Примем, что величина потенциала здесь имеет составляющую в направлении, совпадающем с радиусом круга, и нормальном ему направлении, но в одном из направлений она преобладает. Соответственно образующиеся структуры будут производными от структур, изображенных на рис. 61 и 66, 62 и 67, 63 и 68, 64 и 69, 65 и 70. У возникающих структур магистральными будут те элементы, направление которых соответствует направлению, в котором задан максимум величины потенциала. Некоторые из возможных структур, возникающих при этих условиях, изображены на рис. 78—80; на них показаны в основном лишь элементы первой генерации.

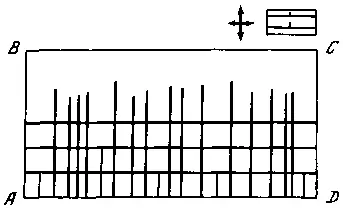
Рис. 75

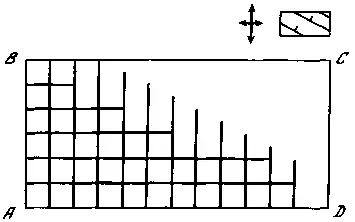
Рис. 76

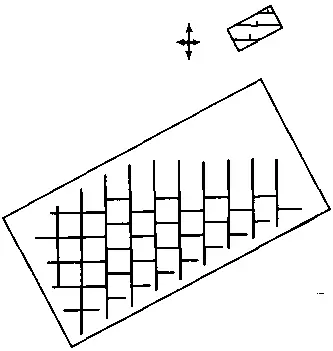
Рис. 77

При сложном рельефе потенциальной функции ее можно графически представить следующим образом: расставить в пространстве множество точек и значения потенциальной функции в каждой точке охарактеризовать индикатрисой. Пример потенциальной функции, заданной таким образом, приведен на рис. 81, там же показана последовательность развития структуры, которая возникнет в этом потенциальном поле при наращивании потенциала.

В этом разделе мы рассмотрели ситуации, когда потенциал был ориентирован только в двух направлениях: x и y (индикатриса-крест). Но тетрагональные решетки могут возникнуть и при других индикатрисах. Например, в виде ромба, эллипса. Но в ситуации с эллипсом возможен вариант, когда в какой-то точке, после того как в главном направлении потенциал будет частично разгружен проходящим рядом элементом, индикатриса в этой точке примет форму окружности. Условия станут изотропными, и элемент, зародившийся в этой точке, может быть ориентирован в любом направлении. Такая ситуация возможна в центрах прямоугольных ячеек. Если индикатриса имеет форму восьмерки, то при появлении элемента в его зоне разгрузки она примет «X»-образную форму. В этом случае параллельная система элементов первой генерации будет разбита поперечными под острыми углами (рис. 82).

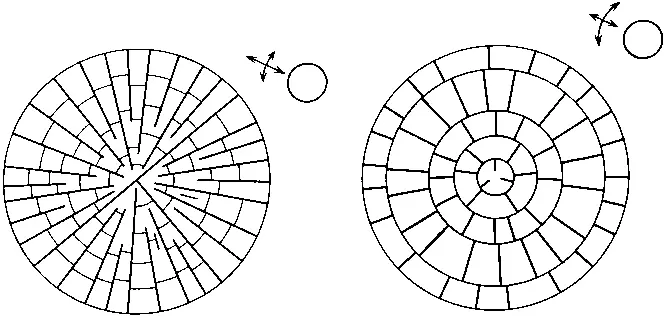
Рис. 78

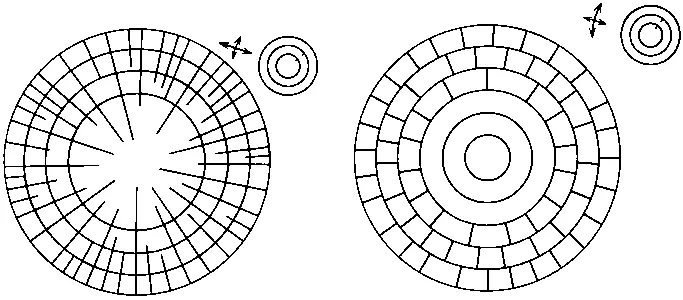
Рис. 79