Сергей Зимов - Азбука рисунков природы

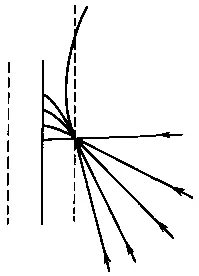
Рис. 101

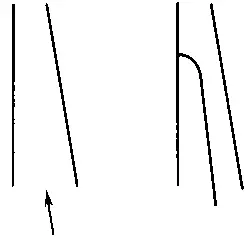
Рис. 102

Рис. 103

Теперь зададим наклонную поверхность потенциального рельефа. Тогда на линии АВ расположится гребень его максимума. Но потенциал здесь будет иметь только одну составляющую в направлении линии АВ. Составляющая перпендикулярная этому направлению на линии АВ краем массива будет полностью разгружена, т. е. у края массива в полосе шириной l потенциальное поле анизотропно. При достижении на линии АВ условия Е = Р здесь будут зарождаться структурные элементы (рис. 104, а). Проникая в глубь массива, они достигнут границы зоны разгрузки элемента АВ. Здесь поле потенциальной функции становится изотропным. Пересекая «по инерции» эту линию, элемент входит в зону с меньшими значениями потенциала и стремится развернуться в зону с большими значениями — назад к линии АВ (рис. 104, б). При этом вершины элементов будут или встречаться, или заходить в зону разгрузки других элементов и подходить к элементам под прямым углом (рис. 104, в). В результате сформируются тройные сочленения. В узлах тройного сочленения элементов зоны разгрузки накладываются, потенциал здесь разгружен по всем направлениям, поэтому при росте значений потенциала новые элементы будут закладываться на выпуклых участках края структуры, перпендикулярно имеющимся элементам, потенциал в этом направлении здесь ими не разгружен (рис. 104, г). Дальнейшее развитие структуры подобно первому этапу: элементы выйдут из зоны разгрузки и начнут разворачиваться обратно и т. д. (рис. 104, д). В этой структуре размер полигонов в направлении смещающейся границы будет выдержанным.

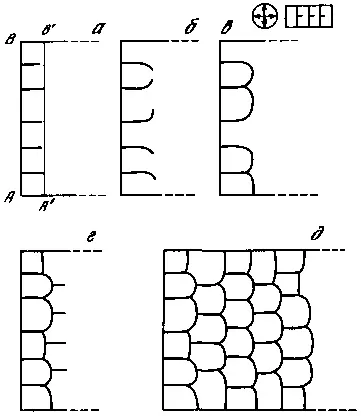
Рис. 104

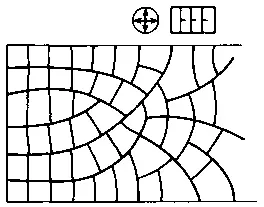
Рис. 105

В рассматриваемой схеме предполагалось, что наклон потенциальной поверхности очень крутой. Быстрый разворот элементов возможен лишь при определенных условиях: чем меньше минимальный радиус разворота, чем меньше их «инерционность» и чем больше наклон потенциальной поверхности, тем быстрее они развернутся. В противном случае будут формироваться структуры, подобные изображенной на рис. 105.

Если потенциальный рельеф задать в виде конуса, то в случае заложения в его вершине тройного сочленения элементов при возможности их быстрого разворота сформируется упорядоченная структура, состоящая из шестиугольников (рис. 106).

Во всех предыдущих схемах и разделах в случае, если один элемент подходил к другому, предполагалось, что они не пересекались. Теперь же зададим, что элементы могут пересекаться. Особенности, накладываемые этим условием, во многих случаях не требуют особого пояснения. Поэтому все рассмотренные выше схемы для различных параметров потенциального поля, скорости развития элементов и т. д. рассматривать не будем. Ограничимся лишь некоторыми примерами. Так, в однородном анизотропном поле в случае моментального образования элементов при этом условии возникнут структуры, изображенные на рис. 107, 108.

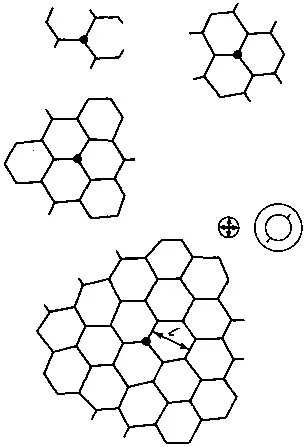
Рис. 106

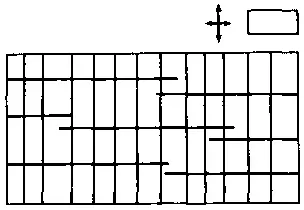
Рис. 107

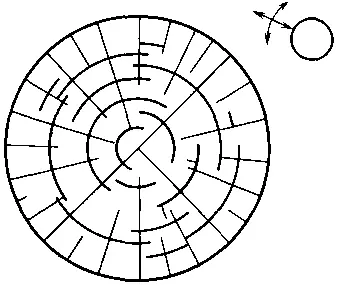
Рис. 108

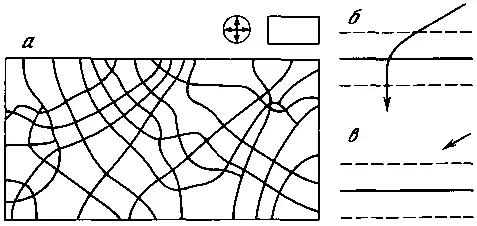
Рис. 109

В изотропном однородном поле при моментальном образовании элементов и условии разгрузки потенциала в направлении, параллельном элементу, возникнет структура, изображенная на рис. 109, а (ср. с рис. 103). Отметим важный момент. В этих условиях при косом заходе одного элемента в зону разгрузки другого он разворачивается и подходит к элементу перпендикулярно, соответственно после пересечения элемента он выйдет из зоны разгрузки (с другой стороны) уже под прямым углом (см. рис. 109, б, в). То есть по рисунку можно определить, куда двигался элемент.

Еще одно специфическое условие. В ранее рассмотренных примерах задавалось, что элемент в зоне разгрузки разгружает составляющую потенциала в направлении, параллельном элементу. В направлении же перпендикулярном величина потенциала оставалась неизменной. Теперь зададим, что в этом направлении возле элемента величина потенциала возрастает (или, что тоже бывает, снижаются значения пороговой функции). В таких условиях при появлении первого коротенького линейного элемента от него тут же перпендикулярно отойдут два новых — возникнет крестообразное сочленение. Новые элементы здесь уже образоваться не смогут, гак как взаимно-перпендикулярные элементы разгружают возле точки своего пересечения потенциал во всех направлениях. При дальнейшем удлинении элементов, как только их вершины отойдут от точки пересечения на величину большую, чем l , возникнут новые элементы — «притоки».

А теперь остановимся на двух примерах, показывающих развитие таких рисунков. Представим прямоугольный массив с однородным изотропным потенциальным полем Е < Р . Зададим границы структурными элементами лишь разгружающими массив (без концентрации у кромки). Искусственно зададим в центре прямоугольника микронеоднородность, в которой появится одиночный элемент, в вершинах которого происходит высокая концентрация потенциала (такие элементы могут двигаться даже при условии Е < Р ). Примем, что элементы не могут подходить один к другому и при встрече вершин стремятся разойтись. Это, например, может произойти, если элемент непосредственно возле своей вершины концентрирует потенциал, а на удалении разгружает его. Можно обеспечить это также тем, что потенциал вокруг вершины частично разгружается, а движется она за счет снижения «прочности» в вершине. При таких условиях сформируется структура, подобная изображенной на рис. 110. При ее разрастании постоянно возникает ситуация конкуренции, опережающее развитие одного элемента сдерживает другой, встречный.

Рассмотрим ситуацию, при которой конкуренция выражена в еще большей степени. Зададим на одной из сторон прямоугольника несколько глубоких затравочных неоднородностей, в которых возникнут элементы. Примем, что в пределах всего массива Е < Р , но поле неоднородно, у стороны с неоднородностями величина потенциала наименьшая. Остальные условия примем такими, как и в предыдущем примере. В этом случае возникшие здесь элементы будут стремиться к противоположной стороне. Причем чем дальше они продвинутся, тем выше будет скорость их движения, так как величина потенциала в этом направлении возрастает. В такой ситуации элемент, «вырвавшийся» вперед, для остальных недосягаем (рис. 111).