Сергей Зимов - Азбука рисунков природы

Улицы городов возникают также не сразу. Обычно граница города медленно, столетиями, отодвигается от его исторического центра и тянет за собой улицы. В противоположность этому, есть города (районы), сформированные эпигенетически: они заложены не как последовательное продолжение старой структуры, а сразу, по единому плану. Многие большие территории заселялись и покрывались транспортными сетями также не сразу. Вспомним движение волны переселенцев в Сибири и в Северной Америке. А биологические структуры? Они часто возникают тоже путем последовательного наращивания клеток от точек, линий и поверхностей роста. А символ строгого порядка — кристаллы? И здесь медленное наращивание, а если нет смещающейся границы структурообразования, то возникает аморфная структура, в ней нет дальнего порядка.

После этих примеров напрашивается вывод, что пространственная упорядоченность возникает при пространственной и, следовательно, временной последовательности в образовании структурных элементов. Порядок в пространстве — это порядок во времени! (?).

Наращивание — важный момент, но только этим не объяснить все многообразие и все детали природных рисунков. Чтобы разобраться во всех сложностях и закономерностях пространственной организации, перейдем к рассмотрению простейших (специально упрощенных) примеров и абстрактных моделей.

Рассмотрим одномерные пространственные структуры. Они могут быть представлены точками, расположенными вдоль линии. Это, например, цепочка островов, телеграфные столбы вдоль дороги, голуби на карнизе, узелки на хлысте бамбука, трещины усыхания на изоляции старого электрического провода или капельки клея на нитке паука. Упорядоченность таких структур выражается в закономерном взаиморасположении этих точек (структурных элементов), т. е. взаимоположение каждого из них точно определено неким законом. В общем виде одномерная упорядоченность может быть охарактеризована как существование определенного пространственного ритма. Простейшая периодичность — повторение элементов через равные интервалы. Этот вид упорядоченности часто встречается или, во всяком случае, часто заметен.

Рассмотрим на примерах, каким путем может появиться такая упорядоченность.

Первый пример. По тропинке катится зубчатое колесо, оставляя упорядоченную цепочку точек. Ее упорядоченность — следствие другой упорядоченности. Из колеса упорядоченность «перекатывается» в тропинку.

Другой пример. Вы идете по заснеженной тропинке, и если идете равномерно, то появится пространственная упорядоченность — ваши следы. И в данном случае она есть следствие другой упорядоченности — периодичности во времени ваших шагов. Подобные структуры часто встречаются в природе. Например, язык отступающего, пульсирующего ледника оставляет последовательность конечных морен.

Еще пример. Дорога вначале была выложена одинаковыми бетонными плитами, а затем заасфальтирована. Если вдруг ударит сильный мороз, то асфальт лопнет, причем по стыкам плит, и дорога покроется трещинами, расположенными на одинаковом расстоянии одна от другой. В данном случае периодическая структура — также «слепок» с другой скрытой структуры. Нас же в наибольшей степени интересует процесс самоорганизации упорядоченных структур, появляющихся при отсутствии какой-либо внешней или первоначальной периодичности.

Представим бесконечно длинный однородный упругий брусок, свободно лежащий на ровной поверхности. Начнем его равномерно охлаждать. При этом в нем возникнут растягивающие напряжения σ x. Как только они достигнут предела прочности, брусок разорвется. Так как условия однородны, то образование разрыва может произойти в любом месте.

До образования разрыва между бруском и поверхностью силы трения (касательные напряжения) отсутствовали — он лежал свободно, и растягивающие напряжения уравновешивались силами внутреннего сцепления в бруске. После разрыва растягивающие напряжения у образовавшегося края бруска перестают уравновешиваться, и под действием этих неуравновешенных сил края бруска сжимаются, разрыв при этом расширяется. В движение будут вовлекаться все большие отрезки бруска. Это будет происходить до тех пор, пока сила трения, появившаяся под движущейся частью бруска (а она пропорциональна длине этой части), не уравновесит упругие силы, действующие со стороны ненарушенной части бруска, после чего движение краев бруска прекратится. Определим распределение растягивающих напряжений в бруске вблизи разрыва. Поместим центр координат в точку разрыва и выделим вблизи ее элементарный отрезок бруска длиной Δx (рис. 13). Запишем для него баланс сил. Небольшим изменением длины бруска за счет образования разрыва, деформациями сдвига в тонком бруске и силой инерции пренебрегаем. С одной стороны, на вертикальную грань отрезка бруска действует внутренняя сила F x= σ xh, где h — толщина бруска, с другой — F x-Δx= σ x-Δxh. Результирующая этих сил Δ F = Δσ xh. Она уравновешивается касательным усилием — силой трения, приложенной к основанию отрезка: Q = T xΔx, где T x— критическое касательное напряжение в основании бруска. Оно зависит от давления бруска на основание и от шероховатости поверхности. Для принятых однородных условий T x= const = K. Приравняв силы, получаем KΔx = hΔσ x, записав dσ x/dx = K/h; после интегрирования, учитывая, что в точке разрыва σ x= 0, получаем σ x = K/h*x. Тут же записываем оговоренное выше условие σ x<= σ пред, т. е. после стабилизации края бруска напряжения вблизи разрыва будут подчиняться линейному закону (рис. 14).

Для нас представляет интерес ширина раскрытия разрыва. По сути, это размер структурного элемента. Рассчитать его несложно. Не вдаваясь в подробности, отметим, что эта величина пропорциональна суммарной разгрузке напряжений вблизи разрыва, суть — высвободившейся при разрыве потенциальной энергии упругонапряженного бруска. Графически ее можно представить площадью фигуры, заштрихованной на рис. 14.

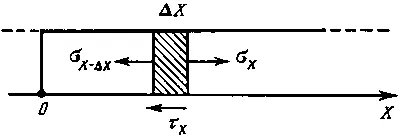
Рис. 13

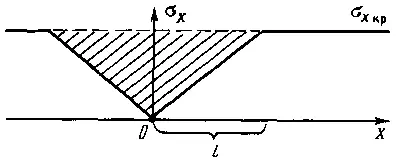
Рис. 14

Итак, образовался первый разрыв. Брусок однородный и равномерно напряжен. Поэтому тут же вслед за первым разрывом в случайных местах образуются и другие разрывы. Если расстояние между двумя разрывами превышает 2l , то между ними останется неразгруженная полоса, и здесь возникнет еще один разрыв. Если это расстояние меньше 2l , то зоны разгрузки соседних разрывов перекроются и новый разрыв между ними не появится.