Лэнс Фотноу - Золотой билет

Геном человека содержит двадцать три пары хромосом, каждая из которых представляет собой двойную цепочку пар оснований. Основания бывают четырех видов – аденин (A), цитозин (C), гуанин (G) и тиамин (T). Цепочки начинаются примерно так: «ACTGATTACA…»; некоторые достигают прямо-таки гигантских размеров. Самая короткая хромосома содержит около 47 миллионов пар оснований, а самая длинная – около 247 миллионов. Современные методы секвенирования ДНК позволяют за один прием обрабатывать участки длиной от 20 до 1000 пар оснований. Ученым приходится секвенировать огромное число коротких кусков, а потом придумывать, как их лучше соединить. Склейка последовательности – задача огромной вычислительной сложности и принадлежит она классу NP: ведь, имея на руках готовую последовательность, можно относительно быстро определить, складывается она из секвенированных участков или нет. Поскольку эффективные методы для поиска оптимального решения пока неизвестны, биологи при составлении карты человеческого генома вынуждены секвенировать избыточное число последовательностей; к сожалению, это не слишком спасает их от ошибок и неясных мест, которых при наличии хорошего алгоритма было бы гораздо меньше.

Последовательности ДНК содержат закодированную информацию о последовательностях матричных РНК, а те, в свою очередь, хранят информацию о синтезе белков. Белки – или, иначе, протеины – играют ключевую роль в работе клеток, формирующих любой живой организм. Для выполнения своих функций протеин должен особым образом свернуться, т. е. принять определенную пространственную форму. Сложный механизм сворачивания биологами пока не разгадан; известно только, что процессом командуют матричные РНК. Решение проблемы равенства P и NP помогло бы продвинуться на пути понимания этого механизма и, как следствие, – лечения и предотвращения болезней.

В некоторых случаях предсказать пространственную структуру белка помогает статистический метод протягивания, работающий с последовательностями РНК. Впрочем, этот метод тоже требует решения NP-задач, хотя и дает нам лишь самое отдаленное представление о механизмах сворачивания.

К классу NP принадлежит и проблема поиска состояния минимальной энергии физической системы – например, множества взаимодействующих магнитных частиц или скопления мыльных пузырей. Эффективно находить такие состояния мы пока не умеем. Но разве это не то же самое, что и состояние равновесия? Нет – потому что в состоянии равновесия энергия физической системы не обязательно падает до минимума.

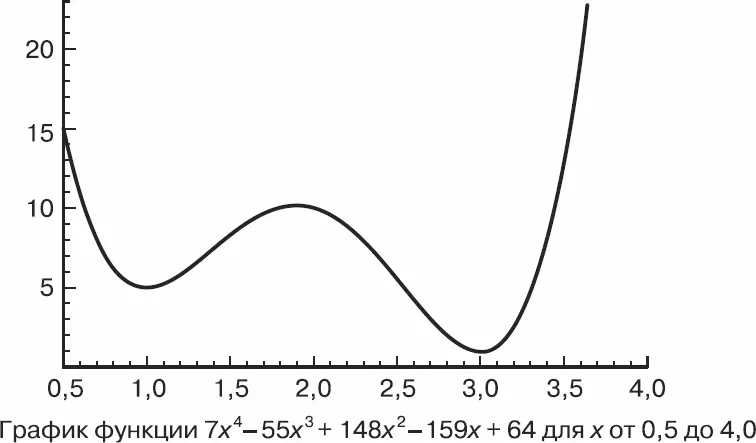
Рис. 3.17.Простейшая физическая система

Рассмотрим простейшую физическую систему: шарик на неровной поверхности (рис. 3.17). При x = 3,0 уровень потенциальной энергии шарика минимален, а при x = 1,0 – нет, хотя шарик будет оставаться в этой точке до тех пор, пока его не толкнут. Таким образом, состояние покоя еще не гарантирует минимального уровня энергии. Поиск состояния минимальной энергии для сложных физических систем – задача чрезвычайно трудная, с которой подчас не справляются не только компьютеры, но и сами физические системы.

С некоторыми особо трудоемкими NP-задачами можно бороться при помощи квантовой механики; подробнее об этом вы узнаете в девятой главе.

Менеджер хедж-фонда ищет наилучшую форму помещения капитала. Покупатель в супермаркете старается уложиться в бюджет. Оба сталкиваются с труднейшей вычислительной задачей из класса NP, решить которую получается далеко не всегда, и часто выбирают совсем не оптимальную стратегию. Каким образом отсутствие эффективных с вычислительной точки зрения алгоритмов в различных сферах рынка сказывается на экономике и на жизни общества в целом? Прекрасный вопрос; к сожалению, достойного ответа на него не может дать никто.

В книге «Игры разума» и в одноименном фильме описывается жизнь известного экономиста Джона Нэша. Нэш доказал, что в любом процессе стратегического взаимодействия нескольких сторон, или игроков, существует состояние равновесия, при котором стратегия каждого игрока такова, что он не выиграет от ее изменения в одностороннем порядке. За свою работу ученый спустя несколько десятилетий получил Нобелевскую премию. Доказательство Нэша не дает нам алгоритм поиска оптимальных стратегий; впрочем, позже выяснилось, что эта поисковая задача обладает огромной вычислительной сложностью. Маловероятно, что различные сферы рынка сами, естественным образом, смогут достичь состояния равновесия; по всей видимости, они так и будут непрерывно перетекать из одного состояния в другое, поскольку люди постоянно меняют стратегии в стремлении добиться наилучших результатов.

В 1928 году выдающийся немецкий математик Давид Гильберт сформулировал свою знаменитую проблему разрешимости – Entscheidungsproblem : существует ли универсальный алгоритм, который для любого математического утверждения определяет, истинно оно или ложно? В 1931 году Курт Гёдель показал, что некоторые утверждения невозможно доказать или опровергнуть ни в одной системе аксиом; спустя несколько лет вдохновленные его результатами Алонзо Чёрч и Алан Тьюринг независимо друг от друга доказали, что универсального алгоритма не существует.

Допустим, у нас есть некое математическое утверждение и нам требуется найти относительно короткое доказательство, которое, к примеру, уместилось бы в тоненькой книжке. Эта задача лежит в классе NP, поскольку оценить длину уже имеющегося доказательства легко, а создать его совсем не просто; будь у нас на руках все возможные доказательства, мы нашли бы искомое обычным перебором. Вот почему математики, которым удалось придумать какое-нибудь хитрое доказательство, становятся знаменитыми.

Определить условия истинности логического выражения тоже иногда бывает очень трудно, даже если выражение это не слишком сложное. Из данной проблемы выросла целая теория, связавшая вместе большинство NP-задач; подробнее мы познакомимся с ней в следующей главе.

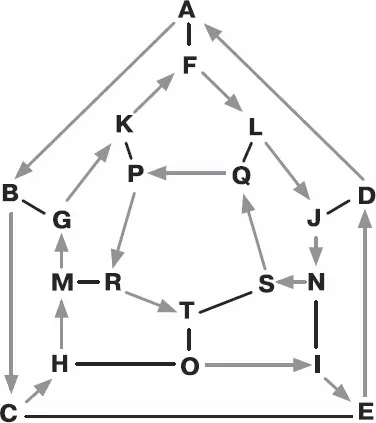
Рис. 3.18.Обход додекаэдра

Психолог проводит эксперимент над математиком. Математика посадили в маленький деревянный сарай; на полу лежит лучина для растопки, рядом стоит стол, а на нем – ведро с водой. Психолог поджигает лучину. Математик хватает ведро и заливает огонь водой.