Лэнс Фотноу - Золотой билет

Помимо зашифрованного текста, хакеры анализируют самую разнообразную информацию – к примеру, время шифрования, которое для разных сообщений может отличаться. Еще вариант – вывести из строя часть системы, как в случае с расплавленной в микроволновке смарт-картой, и надеяться, что сбои приведут к потере конфиденциальности.

Никакой, пусть даже самый стойкий шифр не гарантирует стойкость всей системы; не исключено, что абсолютно надежный протокол мы так и не создадим.

В 1982 году лауреат Нобелевской премии по физике Ричард Фейнман обратил внимание на тот факт, что простого способа смоделировать работу квантовой системы на цифровом компьютере не существует. Из проблемы родилась идея: а что, если вычислительные устройства, основанные на принципах квантовой механики, будут работать намного эффективнее обычных компьютеров?

В последующие десятилетия в результате совместных усилий физиков и кибернетиков (которые вообще часто работают вместе) было доказано, что некоторые задачи – в частности, разложение на простые множители – квантовые компьютеры способны решать несравненно быстрее. Неизвестно, увидят ли когда-нибудь свет даже самые средненькие квантовые компьютеры, не говоря уже о больших и полноценных; неизвестно также, сумеем ли мы корректно оценить их возможности: все это пока находится под большим вопросом. В данной главе речь пойдет о квантовых вычислениях, об их мощности и таких связанных с ними понятиях, как квантовая криптография и телепортация.

Том живет в Бостоне и, конечно, болеет за «Ред Сокс». Днем его любимая команда принимала Нью-Йоркских «Янкиз»; Том был на работе и специально не читал бейсбольные новости. Вернувшись домой, он заказал пиццу, включил телевизор и начал смотреть игру, которая к тому моменту уже давно закончилась. На исходе девятого иннинга у хозяев были заняты вторая и третья база, два игрока были в ауте и один в рандауне. Отбивающий Брайан Хаммер побежал к «дому». Том напряженно замер в надежде, что его команда получит очко, – и вдруг одернул себя: эфир-то не прямой! Очко уже либо заработано, либо нет, только Тому пока об этом не известно. Для него исход по-прежнему не определен: не победа и не поражение, а что-то между ними. Результат игры он узнает чуть позже.

Реальность для Тома определяется тем, что он видит. Он смотрит последний иннинг – а значит, в его мире еще никто не победил. Матч продолжается; и пока не закончится последний розыгрыш, он так и будет находиться в промежуточном состоянии между победой «Ред Сокс» и их поражением.

Сьюзен – ярый фанат «Янкиз». Она тоже записала игру и теперь, как и Том, смотрит ее в оффлайн-режиме и гадает, заработает ли Хаммер победное очко. Для Сьюзен, как и для Тома, результат игры еще не определен; он случаен – ровно до того момента, пока Сьюзен не услышала финальный свисток.

Том и Сьюзен одновременно наблюдают разные случайные события, находясь в 200 милях друг от друга. И все же результат они увидят совершенно одинаковый. И для Тома, и для Сьюзен Хаммер либо заработает победное очко, либо не заработает. Не может быть такого, чтобы в мире Тома Хаммер заработал очко, а в мире Сьюзен – нет. Исход игры никто из зрителей пока не знает, однако оба уверены, что в конце увидят на табло один и тот же счет. Результаты событий, отражаемых на экранах телевизоров Тома и Сьюзен, каким-то загадочным образом связаны друг с другом.

Вы спросите, причем здесь квантовые вычисления? В классических цифровых компьютерах основной логической единицей является бит, или двоичная цифра (от англ. bit – binary digit ). Каждый бит может принимать ровно два значения, например – истина и ложь, или победа и поражение. Базовый элемент квантовых компьютеров – это кубит, или квантовый бит (от англ. qubit – quantum bit ). В отличие от бита, который всегда принимает одно из двух пограничных значений, кубит может находиться в некотором промежуточном состоянии, называемом суперпозицией.

Записанные на телевизор бейсбольные игры – это, конечно, не кубиты, однако с кубитами у них имеется много общего. Пока игра идет, она находится в неопределенном, промежуточном состоянии, и это продолжается вплоть до финального свистка. Затем Том наблюдает окончание игры, и тут уже всякая неопределенность исчезает, поскольку становится ясно, кто выиграл, а кто проиграл. С кубитом дело обстоит аналогичным образом: как только за ним начинают наблюдать, он покидает свое промежуточное состояние и принимает одно из двух пограничных значений, превращаясь в самый обыкновенный бит.

Квантовые биты могут быть определенным образом связаны, или запутаны, – например, так, что при каждом измерении они будут приходить в одно и то же состояние. Нечто подобное происходит и при просмотре записанных на телевизор бейсбольных игр.

Впрочем, на этом совпадения кончаются. В общем случае связи между кубитами намного тоньше и сложней. Управляя запутанными системами кубитов, можно организовывать целые вычислительные процессы.

Состояние бейсбольного матча «ходит» вдоль одной оси: это просто вероятность того или иного исхода.

Рис. 9.1.Бостонская команда

Звездочкой обозначена тридцатипроцентная вероятность победы Бостона. Пока Том смотрит матч, звездочка перемещается; в зависимости от исхода игры она попадет либо в самую левую точку, либо в самую правую.

Состояния кубита образуют окружность с центром в точке пересечения осей «Истина» и «Ложь».

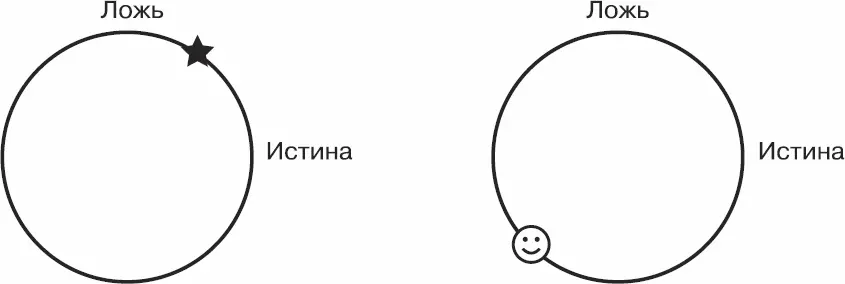
Рис. 9.2.Кубиты

В данном случае звездочка перемещается по двумерной траектории. На рис. 9.2 ее текущие координаты – 0,55 по «Истине» и 0,84 по «Лжи». Координаты вполне могут быть и отрицательными: к примеру, смайлик находится в точке (-0,71; -0,71). Квантовые компьютеры вращают и переворачивают эти окружности и таким образом управляют состояниями кубитов.

Одному кубиту соответствует окружность на плоскости. Двум кубитам требуется четырехмерная окружность; нарисовать ее здесь или даже просто представить в уме было бы довольно затруднительно. В системе из тридцати кубитов размерность пространства будет более триллиона.

Все это наводит на мысль использовать квантовые компьютеры для решения NP-задач. Допустим, нам нужно найти клику размера 50 среди 20000 жителей Королевства. Имея около 500 кубитов, мы сможем воспроизвести сразу все группы размера 50, которые будут обрабатываться параллельно; чтобы отметить клику, квантовый компьютер выполнит определенную последовательность вращений и переворотов.