Ангелина Яковлева - Статистика. Ответы на экзаменационные билеты

Средняя гармоническая простаястроится по формуле:

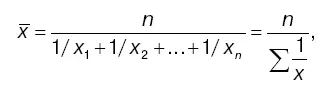
где n — число единиц совокупности или число вариантов;

х — значения варьирующегося признака.

Средняя гармоническая простая используется для несгруппированных данных.

Средняя гармоническая взвешеннаястроится по формуле:

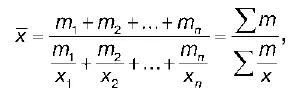
где х — значения варьирующего признака;

m — веса;

n — число единиц совокупности. Среднюю гармоническую взвешенную используют для сгруппированных данных, т. е. когда каждое значение х повторяется различное число раз.

Средняя квадратическая простаястроится по формуле:

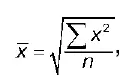
где n — число единиц совокупности или число вариантов; х — значения варьирующегося признака.

Средняя квадратическая простая используется для несгруппированных данных.

Средняя квадратическая взвешеннаястроится по формуле:

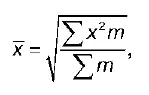
где m – веса;

х – значения варьирующего признака.

Среднюю квадратическую взвешенную используют для сгруппированных данных.

Данные формулы используются редко, в специальных расчетах.

Средняя геометрическая простаястроится по формуле:

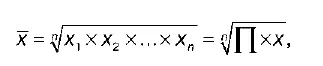
где n – число единиц совокупности или число вариантов;

х – значения варьирующегося признака. Средняя геометрическая простая используется для несгруппированных данных.

Средняя геометрическая взвешеннаястроится по формуле:

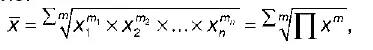
где х – значения варьирующего признака;

m – веса;

n – число единиц совокупности или число вариантов. Различные формулы средних величин можно объединить в одной формуле – формуле степенной средней:

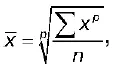
где р – порядок средней.

Медианой М е называется варианта, которая делит ранжированный вариационный ряд на две равные части, из которых значение одной половины меньше медианы, а значения другой – больше медианы.

Медиана для несгруппированных данных при нечетном числе вариантов ( n = 2k+ 1 ), определяется как M e = x k + 1, а при четном числе вариантов (n = 2k ), медиана определяется по формуле:

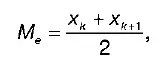
Медиана для сгруппированных данных рассчитывается по формуле:

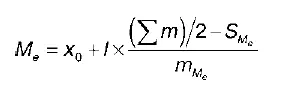
где х 0– это нижняя граница медианного интервала;

/– величина медианного интервала;

em / 2 – полусумма всех частот;

S Me – накопленная частота, предшествующая медианному интервалу;

m Ме – частота медианного интервала.

Медиана рассчитывают наряду со средней величиной или вместо нее, когда в ряду данных присутствуют открытые или неравные интервалы. Это не влияет на точность медианы, однако, влияет на точность величины.

Модой М 0 называется варианта, которая имеет наибольшую частоту по сравнению с другими частотами. В дискретно-вариационном ряду мода – это та варианта, которой соответствует наибольшая частота.

В интервальном вариационном ряду с равными интервалами моду определяют по формуле:

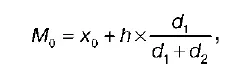
где х 0– это нижняя граница модального интервала;

h – величина модального интервала;

d 1– разность между частотами модального и предмодального интервалов;

d 2– разность между частотами модального и послемодального интервалов.

Мода рассчитывается в тех случаях, когда невозможно или нецелесообразно рассчитывать среднюю величину по обычным формулам.

Асимметрией распределенияназывается несоразмерность, т. е. нарушение соответствия в расположении частей одного целого относительно средней линии или центра. На графике асимметрия распределения определяется как вытянутость одной из ветвей распределения. Асимметрия распределения возникает в связи с различной частотой появления вариант больших или меньших моды (т. к. мода соответствует вершине распределения) под влиянием преобладающего действия определенных факторов. Таким образом, наличие асимметрии говорит о неустойчивости распределения совокупности в связи с преобладающим воздействием какой-либо группы факторов.

Асимметрия распределения легко обнаруживается и измеряется на основе разницы между средней величиной и модой. В умеренно асимметричных распределениях мода и средняя образуют интервал, в пределах которого находится медиана. Если разделить этот интервал на 3, то медиана отстоит от моды на 2/3, а от средней – на 1/3.

Для измерения асимметрии рядов распределения применяется эмпирический коэффициент асимметрии:

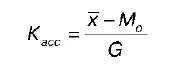
где x— – простая средняя;

М о– мода;

G – среднеквадратическое отклонение.

К абсолютным показателям вариации относятся:

1) вариационный размах ( R );

2) среднее абсолютное (линейное) отклонение (в);

3) дисперсия ( G 2 );

4) среднеквадратическое отклонение ( G ).

Вариационный размах R — это разность между

наибольшей и наименьшей вариантами вариационного ряда:

R = х max– х min

Вариационный размах является наиболее простой характеристикой рассеяния вариационного ряда. Недостатки данного показателя:

1) неточно характеризует колеблемость, потому что зависит только от двух значений признака;

2) зависит от объема совокупности, т. е. с увеличением объема совокупности увеличивается вероятность размера вариационного размаха.

Среднее абсолютное отклонение в— это вели чина, которая рассчитывается как среднее арифметическое абсолютных отклонений в данной совокупности.