Ангелина Яковлева - Статистика. Ответы на экзаменационные билеты

1) количественныепоказатели, характеризующие объем того или иного явления.

К ним относятся:

а) q – физический объем товарооборота (количество проданной продукции в натуральном выражении);

б) q – физический объем продукции (количество произведенной продукции на предприятии);

в) t – число рабочих;

г) h – посевная площадь и др. Количественные показатели получают путем подсчета;

2) качественныепоказатели характеризуют уровень явления в расчете на ту или иную единицу совокупности.

К ним относятся:

а) р – цена единицы товара (себестоимость);

б) z – себестоимость единицы продукции (затраты на производство единицы продукции);

в) t – трудоемкость единицы продукции (затраты рабочего времени на производство единицы продукции);

г) w – производительность труда (выработка продукции в единицу времени);

д) у – урожайность;

3) суммарные(итоговые, количественно-качественные) показатели, характеризующие суммарные, общие размеры исследуемого явления.

К ним относятся:

а) S – товарооборот:

S = p × q ;

б) Т – затраты рабочего времени (труда) на производство всей продукции:

Т = t × q ;

в) С – затраты на производство продукции:

С = z × q ;

г) V – валовой сбор с/х культур по видам:

V = y × n .

Индивидуальный индекс– это отношение величины показателя в отчетном или текущем периоде к величине того же показателя в базисном периоде:

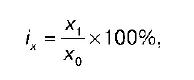
где i – индивидуальный индекс;

х — любой индексируемый показатель (качественный, количественный, качественно-количественный);

1 – отчетный или текущий период;

х 1– сравниваемый уровень;

0 – базисный период;

х 0 – базисный уровень.

Индивидуальные индексы строятся для соизмеримых однородных совокупностей и чаще всего выражаются в процентах.

Индивидуальный индекс характеризует изменение объема или уровня исследуемого показателя в отчетном периоде по сравнению с базисным. Если i x < 100 %, то уровень индексируемого показателя снизился по сравнению с базисным периодом. Если i x> 100 %, то уровень индексируемого показателя увеличился по сравнению с базисным периодом. Если i x= 100 %, то уровень индексируемого показателя остался прежним.

Примеры индивидуальных индексов:

1) индивидуальный индекс цен:

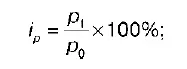
2) индивидуальный индекс физического объема товарооборота:

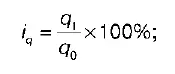
3) индивидуальный индекс товарооборота:

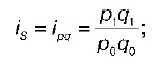
В связи с тем, что индивидуальные индексы используются для изучения динамики индексируемого показателя за короткие и более продолжительные периоды, возникает необходимость исчисления системы последовательных индексов. Различают два метода последовательного индексирования.

1. Метод постоянной (фиксированной) базы.

Согласно данному методу один из периодов, находящихся в знаменателе, принимается в качестве базисного, а остальные, находящиеся в числителе, последовательно меняются.

Предположим, что имеются данные р 0, р 1, …, р n-1, p n. Тогда система индивидуальных индексов с постоянной базой может быть записана следующим образом:

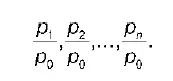
Это система базисных индексов. Индексы этой системы называются базисными и показывают, как изменяется цена по мере увеличения длительности рассматриваемого периода по отношению к одной базе.

2. Метод меняющейся (переменной) базы.

Согласно данному методу каждая индексная система исчисляется на основе своей базы по определенному порядку: в качестве базы индекса принимается предшествующий i -ый период.

Система индексов меняющейся базы может быть записана следующим образом:

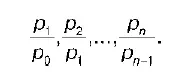
Эта система цепных индексов. Индексы этой системы называются цепными, они характеризуют цену от одного периода к другому.

В связи с тем что статистика часто имеет дело с несоизмеримыми совокупностями, для изучения динамики таких совокупностей используют общие индексы или собственно индексы. Они строятся в агрегатной форме и в средней форме.

Агрегатная форма общего индекса качественных показателей.

Рассмотрим агрегатную форму общего индекса цены. Первоначально эти индексы строились по формулам, предложенным учеными Г. Дюто и П. Карли. Однако эти формулы обладали рядом недостатков, поэтому позднее были предложены другие формулы, например формула Ласпейраса:

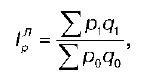
где р — индексируемая величина (цена);

q — количество проданных товаров в натуральном выражении (веса).

В настоящее время именно эта формула используется при изучении динамики цен. Этот индекс характеризует изменение цен в среднем по совокупности товаров в отчетном периоде по сравнению с базисным.

Общий индекс цены можно также определить по формуле Пааше:

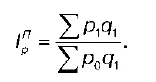
Эта формула длительное время использовалась в СССР при изучении динамики цен. Но с переходом к рыночной экономике стала существенно изменяться структура потребительских расходов населения, т. е. на динамику цен существенное влияние стало оказывать изменение параметра q.

Правило взвешивания общих индексов качественных показателей.

Общий индекс качественных показателей в агрегатной форме взвешивается по весам отчетного периода. Например, общий индекс себестоимости в агрегатной форме:

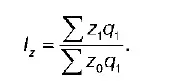
Общий индекс урожайности в агрегатной форме:

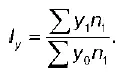
Агрегатная форма общих индексов количественных показателей.Рассмотрим агрегатную форму общего индекса физического объема товарооборота (q). I qможет быть построен по формуле Ласпейраса, которая является основной: