Ангелина Яковлева - Статистика. Ответы на экзаменационные билеты

Одной из задач статистического исследования зачастую является задача исследования группы однородных объектов, явлений или процессов относительно некоторого качественного или количественного признака, характеризующего эти объекты.

При решении данной задачи можно провести сплошное обследование, т. е. обследовать каждый из объектов данной совокупности относительно изучаемого признака.

Выборочное наблюдение– это такой тип несплошного наблюдения, при котором обследованию подвергаются не все единицы изучаемой совокупности, а лишь отобранные в определенном порядке.

Применение выборочного наблюдения способствует:

1) экономии времени и средств в результате сокращения объема работ;

2) минимизации порчи или уничтожения исследуемых объектов;

3) возможности детального исследования каждой единицы наблюдения при неосуществимости охвата всех единиц;

4) достижению большей точности результатов обследования.

Основные понятия выборочного наблюдения.

Генеральная совокупность(N) – это совокупность объектов, явлений или процессов, из которых производится выборка.

Выборочная совокупность (выборка) (п) – это совокупность случайно отобранных объектов из генеральной совокупности.

Генеральная средняя(x) – средняя величина признака для генеральной совокупности.

Выборочная средняя(x) – средняя величина признака для выборочной совокупности.

Генеральная доля(p) – отношение числа единиц генеральной совокупности, обладающих изучаемым признаком, ко всей генеральной совокупности.

Выборочная доля(w) – отношение числа единиц выборочной совокупности, обладающих изучаемым признаком (m), к объему выборочной совокупности:

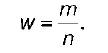
Одним из основных требований к формированию выборочных совокупностей является требование репрезентативностивыборки, т. е. для характеристики по данным выборочной совокупности интересующего исследователей признака генеральной совокупности необходимо, чтобы единицы выборки в достаточной степени обладали этим признаком.

Ошибки выборки.

В процессе всякого наблюдения возникают ошибки регистрации. При выборочном наблюдении возникают специфические ошибки – ошибки репрезентативности (или представительности) выборки.

Ошибка репрезентативности– это разность между обобщающими выборочными показателями и соответствующими показателями генеральной совокупности. Например, для показателя средней ошибка репрезентативности равна модулю разности между выборочной средней и генеральной средней:

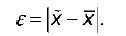
Для показателя доли ошибка репрезентативности равна модулю разности между выборочной долей и генеральной долей:

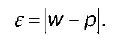
Ошибки репрезентативности выборки делятся на случайные и систематические.

Систематические ошибки выборки направлены в одну определенную сторону (либо в сторону увеличения, либо в сторону уменьшения). Они могут быть преднамеренными и непреднамеренными.

Задача статистики состоит в избежании ошибок репрезентативности, в устранении причин их появления. Также статистика определяет величину случайных ошибок репрезентативности и устанавливает их возможные пределы.

Для формирования выборочной совокупности применяются различные способы отбора.

1. Отбор, при котором генеральная совокупность не разбивается на части:

1) простой случайный повторный отбор. Он характеризуется следующими чертами:

а) отбор единиц выборочной совокупности производится из всей генеральной совокупности;

б) отбор носит случайный характер;

в) единицы генеральной совокупности, попавшие в выборочную совокупность, вновь возвращаются в генеральную совокупность после изучения;

2) простой случайный бесповторный отбор. Он характеризуется следующими чертами:

а) отбор единиц выборочной совокупности производится из всей генеральной совокупности;

б) отбор носит случайный характер;

в) единицы генеральной совокупности после об следования не возвращаются в генеральную совокупность.

В случае применения простого случайного отбора все единицы генеральной совокупности имеют одинаковую вероятность попасть в выборочную совокупность.

2. Отбор, при котором генеральная совокупность разбивается на части:

1) типический отбор, характеризующийся следующими чертами:

а) вся генеральная совокупность разбивается на типически однородные группы или части;

б) отбор единиц производится не из всей генеральной совокупности, а из отдельных типичных групп либо механически, либо случайно.

При типическом способе отбора в выборочную совокупность попадают все представители типических групп, что обеспечивает большую репрезентативность и точность полученных результатов. Одной из предпосылок применения типического отбора являются большое разнообразие генеральной совокупности и ее элементов и значительная неоднородность изучаемых при этом признаков. Его применение связано со сложными социально-экономическими явлениями. Типический отбор является достаточно дорогим, но самым точным способом отбора;

2) серийный отбор, характеризующийся следующими чертами:

а) вся генеральная совокупность разбивается на части (серии или гнезда);

б) отбор единиц генеральной совокупности производится целыми сериями;

в) наблюдению подвергаются все без исключения единицы отобранной серии;

г) отбор носит случайный характер; Серийный отбор является менее точным способом отбора, однако его легче организовать;

3) механический отбор, который характеризует ся следующими чертами:

а) отбор осуществляется из всей генеральной совокупности;

б) отбор производится по механическому принципу (по списку, в шахматном порядке, по географическому признаку, в порядке убывания или возрастания).

Механический отбор является более точным, чем случайный, однако уступает типическому отбору.

На практике также часто применяется комбинированный отбор, при котором сочетаются указанные выше способы отбора.

Существуют два способа распространения данных выборочной совокупности на всю генеральную совокупность: