Эмиль Ахмедов - О рождении и смерти черных дыр

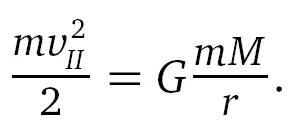
Здесь m и M – это массы рассматриваемых предмета и планеты соответственно; G – константа Ньютона; r – радиус рассматриваемого небесного тела.

Некоторые ученые уже на рубеже XVIII и XIX веков задумались над тем, как должны относиться радиус и масса планеты, чтобы даже свет не смог покинуть ее. То есть чтобы вторая космическая скорость для этого гравитирующего тела была больше скорости света v II ≥ c ≈ 300000 километров в секунду.

Из выписанных формул видно, что радиус такой планеты должен быть меньше, чем 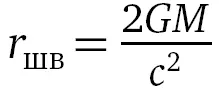– радиус Шварцшильда для данной массы. Он назван в честь ученого, который первым нашел решение уравнений общей теории относительности, описывающее геометрию пространства-времени снаружи гравитирующего тела, имеющего форму шара.

Интересно, что из неверных соображений, с использованием лишь формул из ньютоновской физики, мы получили верный ответ для радиуса черной дыры соответствующей массы. Эти соображения неверны по той причине, что в сильных гравитационных полях и при скоростях, близких к скорости света, уже нельзя пользоваться такими выражениями для кинетической и потенциальной энергий, как использовались выше.

И все же полученная формула для размера черной дыры при заданной массе верна и будет нам полезна. Нетрудно посчитать, например, что для звезды с массой Солнца 2 · 10 30килограмм радиус Шварцшильда приблизительно равен трем километрам. Сравните эту величину с настоящим размером Солнца – 700000 километров. В то же время для планеты с массой Земли радиус Шварцшильда равен нескольким миллиметрам.

Если какая-то сила сожмет небесное тело до соответствующего его массе радиуса Шварцшильда, то оно настолько искривит пространство-время, что даже свет не сможет его покинуть. Это и означает, что тело станет черной дырой. При каких условиях такие сжатия возможны и как они происходят, мы обсудим в следующих главах, а сейчас определим метод, которым мы будем изучать геометрию пространства-времени.

Как известно, пространство-время, в котором мы живем, имеет четыре измерения. То есть для определения какого-то события (точки в пространстве-времени), скажем прохождения светового цуга [1] Цуг – пакет электромагнитных волн. на некотором расстоянии от гравитирующего тела в некоторый момент времени, необходимо задать три пространственных координаты, определяющих данное положение цуга в пространстве, и одну временную координату, определяющую данный момент времени.

Изобразить все четыре измерения на листе бумаги не представляется возможным. Поэтому если мы хотим наглядности, необходимо сделать некоторые упрощения. Каждую точку пространства в фиксированный момент времени можно определить по расстоянию от нее до начала координат, а также по двум углам, которые являются аналогами долготы и широты на глобусе и определяют направление радиус-вектора из начала координат в обсуждаемую точку. Это и есть три координаты, которые необходимы для определения пространственного положения события в пространстве-времени (рис. 2).

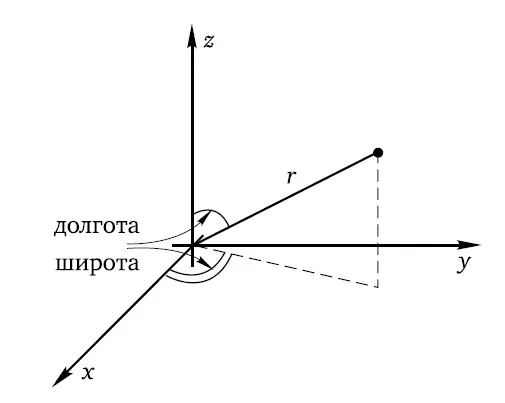
Рис. 2. Здесь изображен пространственный срез – «фотография» пространства, то есть «один из кадров фильма», показывающего, как ситуация развивается во времени. Обычно положение точки в таком пространстве определяют с использованием декартовых координат (х, у, z). Однако есть и другой общепринятый способ определения ее положения в пространстве – через расстояние от начала координат и долготу с широтой

Ниже мы всегда будем рассматривать движения тел и света строго по радиусу, то есть без изменения долготы и широты. Также мы будем рассматривать идеальные сферические звезды, планеты или пылевые облака. В этом и состоит наше упрощение, так как в реальности пылевые облака, падающие на звезды, или даже гравитационные поля вращающихся черных дыр не обладают симметрией сферы [2] Более того, сферически симметричная ситуация крайне неустойчива по отношению к малейшему возмущению. Из-за приливных сил, которые подробнее обсуждаются ниже, любое возмущение, нарушающее сферическую симметрию, будет только расти, приводя к ее полному разрушению. Однако можно показать, что невращающаяся черная дыра сферически симметрична и устойчива по отношению к таким возмущениям, что сильно упрощает нашу задачу. .

Для наших целей главное, что, изображая пространство-время при таком упрощении, мы можем забыть про долготу и широту каждого события и рисовать только временную координату с · t и длину радиус-вектора события r (рис. 3). То есть в таком случае обсуждаемое изображение пространства-времени будет иметь два, а не четыре измерения.

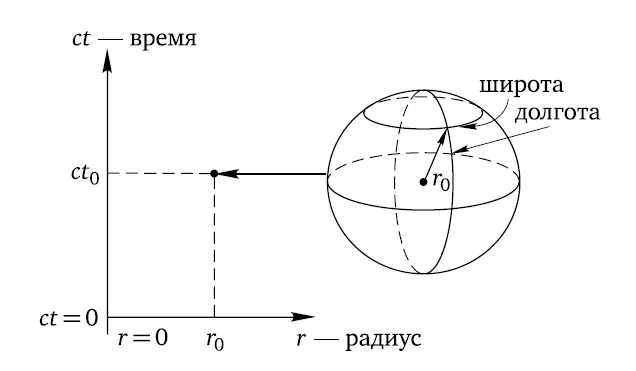
Рис. 3. Если изображать на плоскости только временную координату с · t события и его расстояние r до центра системы координат, то каждая точка такой плоскости может представлять любое положение на сфере радиуса r в пространстве, то есть с любым значением долготы и широты. Иными словами, каждая точка нарисованной здесь плоскости суть двумерная сфера. Следует подчеркнуть, что на самом деле здесь изображена полуплоскость, так как r может принимать только неотрицательные значения

► Для тех, кто знаком со специальной теорией относительности, упомянем о еще одном допущенном упрощении. Дело в том, что мы изображаем пустое пространство – время (ct, r) на обыкновенной евклидовой плоскости (x, y). На такой плоскости расстояние Δ l между двумя точками (ct 1, r 1) и (ct 2, r 2), разделенными пространственным Δx =Δ r =r 1−r 2и временным Δ y= c Δ t = c (t 1−t 2) смещениями, вычисляется с помощью теоремы Пифагора:

Δl 2= Δy 2+Δx 2= c 2Δt 2+Δr 2.

При этом, как следует из совокупности экспериментальных данных, такое расстояние в пространстве – времени следует вычислять по формуле Δs 2=c 2Δt 2−Δr 2. Отличие в знаке существенным образом сказывается на аналитических вычислениях и свойствах геометрии пространства – времени. Учитывая это, последующее геометрическое моделирование вполне адекватно описывает физику черных дыр. ◄

Далее наши рассуждения будут достаточно строгими, хотя мы и будем использовать только наглядные геометрические образы без сложных аналитических математических обоснований, выходящих за рамки школьного курса. Рисуя картинки в этой книге, мы будем руководствоваться здравым смыслом и минимальным количеством данных, следующих из совокупности опытных фактов.