Елена Михеева - Практикум по информационным технологиям в профессиональной деятельности

На нижней панели (шаблонов) расположены кнопки, предназначенные для вставки шаблонов или структур, включающих символы типа дробей, радикалов, сумм, интегралов, произведений, матриц и различных скобок или соответствующие пары символов типа круглых и квадратных скобок. Во многих шаблонах содержатся специальные места, в которые можно вводить текст и вставлять символы. В редакторе формул содержится около 120 шаблонов, сгруппированных в палитры. Шаблоны можно вкладывать один в другой для построения многоступенчатых формул.

Назначение верхних кнопок панели «Редактор формул»

(согласно нумерации кнопок панели редактора на рис. 6.1):

1 – вставка символов отношений;

2 – вставка пробелов и многоточий в формулу;

3 – надсимвольные элементы, позволяющие добавлять к математическим переменным примы, крышки, черту или точку;

4 – вставка операторов в формулу;

5 – вставка стрелок в формулу;

6 – вставка логических символов в формулу;

7 – вставка символов теории множеств;

8 – вставка в формулу разных символов (символы дифференциального исчисления, символы градуса, угла, перпендикуляра и др.);

9 – вставка строчных букв греческого алфавита;

10 – вставка прописных букв греческого алфавита.

Задание 6.2. Используя кнопки нижнего ряда, набрать формулы по образцам

Назначение нижних кнопок панели «Редактор формул»

11 – вставка в формулу шаблонов разделителей:

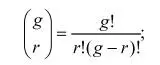
12 – вставка шаблонов дробей и радикалов в формулу:

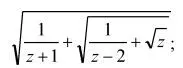
13 – создание в формуле верхних и нижних индексов:

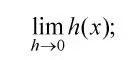
14 – создание сумм в формуле:

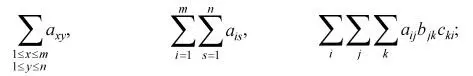
15 – вставка интегралов в формулу:

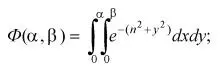
16 – создание математических выражений с чертой сверху и снизу:

17 – создание стрелок с текстом в формуле:

18 – вставка произведений и шаблонов теории множеств в формулу;

19 – вставка шаблонов матриц в формулу. Шаблоны этой палитры позволяют создавать векторные столбцы, определители, матрицы и другие макеты типа таблиц.

Задание 6.3. Создать формулу следующего вида:

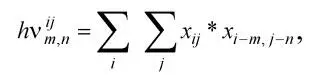
пользуясь кнопками:

– кнопка 13, положение 12 (для ввода левой части формулы);

– знак «равно» и символ «х» ввести с клавиатуры;

– кнопка 14, положение 5 (знак суммы);

– кнопка 13, положение 2 (ввод нижних индексов);

– ввести символ * с клавиатуры (или кнопка 4, положение 5);

– кнопка 13, положение 2 (ввод нижних индексов).

Задание 6.4.Создать формулу для вычисления суммы платежей

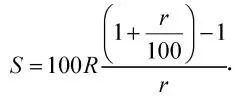
Вставить эту формулу в колонтитул методом копирования. Сохранить созданный файл в папку группы

Задание 6.5.Используя Мастер формул, набрать формулы по образцам:

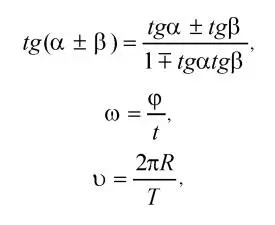
Дополнительные задания

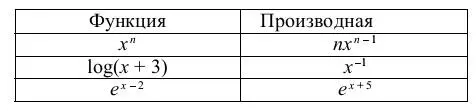
Задание 6.6.Набрать формулы по образцу, используя таблицу символов (Вставка/Символ) (рис. 6.2) и преобразователи в верхний/ нижний индексы

Краткая справка. Для настройки панели инструментов ввода верхних и нижних символов (х 2 и х 2) необходимо вызвать команду Сервис/Настройка/Команды/Формат. Преобразователи в верхний/ нижний символы, представленные иконками х 2и х 2, перетащите левой кнопкой мыши на панель инструментов Word, после чего закройте меню Настройка.

Образец задания

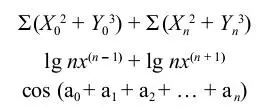
Задание 6.7.Набрать текст и формулы по образцу

Коэффициент корреляции Пирсона используется как мера линейной зависимости между множеством зависимых переменных у и множеством независимых переменных х. Значение коэффициента заключено в пределах от -1,0 до 1,0 и определяется по следующей формуле:

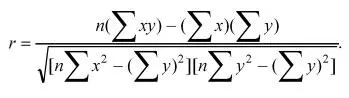
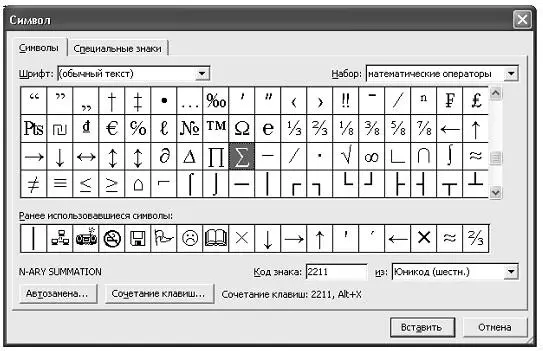
Pис. 6.2. Вставка символа Σ

Задание 6.8.Набрать текст и формулы по образцу

Пример 1.В прямоугольном треугольнике ∆АВС известны длина гипотенузы АВ, равная числу 12,5, и косинус угла АВС, равный числу 44/ 125. Найти величины синуса угла САВ и площадь треугольника.

Дано: С= 12,5 и cos β = 44/ 125.

Найти: sinα и S.

Решение: имеем sin α= a/c = cos β= 44/ 125= 0,325;

a= c* sin α= 12,5 * 0,325 = 4,4;

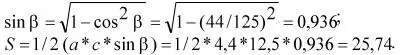
Ответ: 0,325; 25,74.

Пример 2.В условиях предыдущей задачи найти периметр треугольника и радиус вписанной в него окружности.

Решение: имеем b=c * sin β = 12,5 * 0,936 = 11,7.

Периметр 2p= a+ b+ c= 4,4 + 11,7 + 12,5 = 28,6.

p= 14,3; S = p * r; r= S / p = 22,74 / 14,3 = 1,8.

Ответ: 28,6; 1,8.

Пример 3.В треугольнике даны длины трех сторон, равные числам 41, 84, 85. Вычислить радиус вписанной и удвоенный радиус описанной окружностей.

Дано: a= 41, b= 84, c= 85.

Найти: r и R.

Pешение: радиусы r и R легко выражаются через площадь S треугольника. Кроме того, площадь можно найти по формуле Герона.

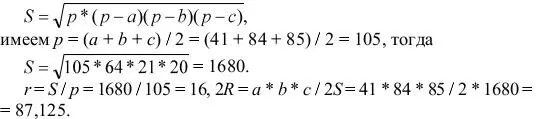
Oтвет: 16; 87,125.

Задание 6.9.Набрать текст и формулы по образцу

Образец задания

Точки Х 1= –1, Х 2= 5/ 4, Х3= 2 делят числовую ось на четыре промежутка.