Лэнс Фотноу - Золотой билет. P, NP и границы возможного

Правительства усердно разрабатывают законы для защиты населения от последствий внедрения алгоритма, однако научно-технический прогресс назад не развернешь. Человек адаптируется быстро; по данным соцопросов, сейчас уже мало кто мечтает повернуть время вспять и перенестись в старый добрый 2012-й, в «до-урбанскую» эру.

Трудно представить, что один-единственный алгоритм способен полностью перевернуть нашу жизнь. Неужели все, что можно описать словами, можно и создать? Неужели можно без труда получать практически любые знания? Звучит невероятно, и именно поэтому большинство ученых не верят в равенство P и NP и полагают, что у нас никогда не будет ни урбанского, ни еще какого-нибудь универсального алгоритма.

Впрочем, рассказанные в этой главе сказки вполне могут стать реальностью – вне зависимости от того, равны классы P и NP или не равны. Конечно, для этого нам потребуется больше времени; к тому же в отсутствие волшебной программы, позволяющей решать сразу все задачи, придется бороться с каждой проблемой отдельно. Однако человеческая изобретательность не знает границ, так что мы в конце концов найдем способ реализовать все свои мечты.

Лучший способ получить наглядное представление о классах P и NP – отправиться в воображаемое Королевство заклятых друзей, в котором любые два жителя либо дружат, либо враждуют.

В Королевстве проживает двадцать тысяч человек. Глядя на каждого из них в отдельности, ничего такого не подумаешь… однако стоит только свести двух жителей вместе – и происходит нечто совершенно необъяснимое: они или немедленно проникаются взаимной симпатией и тут же становятся близкими друзьями, или с первого взгляда превращаются в злейших врагов. Никто и никогда не видел, чтобы между двумя жителями сложилось нечто среднее между дружбой и враждой (как можно было бы заключить из названия «заклятые друзья»): они всегда или дружат взахлеб, или терпеть друг друга не могут.

Никакой системы здесь не наблюдается. Друг вашего друга – точно так же, как и враг вашего врага – может быть вам другом, а может и врагом. Зависимость от пола, расы, вероисповедания и социального статуса тоже вроде бы отсутствует; известно только, что друзей у жителей Королевства обычно намного меньше, чем врагов.

В интернете можно найти массу информации о том, кто с кем дружит. Специалисты факультета компьютерных наук Королевского технологического института проанализировали данные социальных сетей, включая Facebook и Twitter , и составили практически полную базу друзей и врагов в Королевстве. В данной главе мы поговорим о том, как эти данные можно использовать.

Выберем наугад двух жителей Королевства; пусть их зовут Элис и Джордж. Маловероятно, что Элис и Джордж дружат. Возможно, между ними существует связующее звено – общий друг Боб. А возможно, и нет. Исследователи Королевского технологического нарисовали схему, в которой каждому жителю Королевства соответствует один элемент; если жители дружат, то соответствующие элементы соединяются на схеме линией. Один из фрагментов схемы выглядел примерно так:

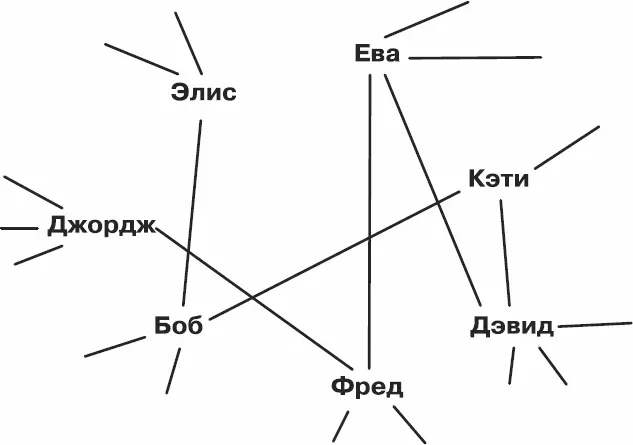
Рис. 3.1.Дружеские связи в Королевстве

Чтобы добраться от Элис до Джорджа, нужно пройти по цепочке из шести связей: Элис дружит с Бобом, Боб – с Кэти, Кэти – с Дэвидом, Дэвид – с Евой, Ева – с Фредом, а Фред – с Джорджем. Исследователи задумались: можно ли любую пару жителей соединить относительно короткой цепочкой дружеских связей? Проявится ли здесь феномен «тесного мира»? Кстати, название феномена пошло вовсе не от аттракциона в Диснейленде, а от слов «мир тесен», которые мы обычно произносим, когда знакомимся с кем-то и выясняем, что нас связывает нечто общее (пусть даже очень отдаленно).

В 1967 году психолог Стэнли Милгрэм поставил свой знаменитый эксперимент по проверке теории «тесного мира». Сначала он выбрал некоего биржевого маклера, проживающего в Бостоне. Имя маклера сохранялось в секрете; для удобства назовем его Том Джонс. Далее совершенно случайным образом в Небраске были выбраны сто держателей акций. Потом – сто людей, не являвшихся акционерами. И, наконец, в Бостоне по объявлению в газетах были найдены еще сто участников. Вторая группа из Небраски и группа из Бостона не имели никакого отношения к инвестиционному миру. Каждому из трехсот участников Милгрэм отослал пакет, в который вложил список инструкций, реестр и пятнадцать почтовых открыток с маркой, адресованных ему в Гарвардский университет. Инструкции выглядели так:

1. Занесите свое имя в реестр.

2. Заполните одну из открыток и бросьте ее в почтовый ящик.

3. Если вы лично знаете бостонского биржевого маклера по имени Том Джонс, перешлите пакет ему.

4. В противном случае выберите среди своих знакомых кого-нибудь, кто, по-вашему, с большей степенью вероятности знает Тома Джонса и чье имя пока не значится в реестре, и перешлите пакет ему (или ей).

Из трехсот участников двести семнадцать переслали пакет своим друзьям. Шестьдесят четыре письма в конце концов добрались до цели, т. е. до Тома Джонса. Средняя длина цепочки оказалась равна 5,2; в результате возникло понятие «шесть степеней отчуждения», означающее, что любых двух человек на планете в среднем разделяет цепочка из шести связей. Отдельные аспекты эксперимента подверглись резкой критике; впрочем, Милгрэм и сам не возводил феномен шести степеней в статус закона, однако его эксперимент показал, что мы связаны гораздо теснее, чем можно было бы ожидать.

Придумывая различные определения понятия связи – более специфические, чем простое знакомство, – можно исследовать и анализировать людские сообщества. Иногда таким образом возникают салонные игры, в которых требуется вычислить расстояние от произвольного человека до некой «центровой» персоны, обладающей, как правило, большим количеством связей. В 1994 году Кевин Бэйкон, выступая в поддержку своего фильма «Дикая река», в шутку заметил, что все актеры в Голливуде снимались либо с ним самим, либо с теми, кто с ним снимался. Тут же родилась игра под названием «Шесть шагов до Кевина Бэйкона», цель которой – найти кратчайший путь между заданным актером и Бэйконом через актеров, с которыми они вместе снимались. Для многих актеров путь до Бэйкона (и, соответственно, друг до друга) оказался очень коротким. Например, Чарли Чаплин находится от Бэйкона всего в трех шагах: в 1967 году он снял фильм «Графиня из Гонконга», в котором сам сыграл второстепенную роль; графиню играла Софи Лорен, которая в 1979 году снялась в малоизвестном фильме «Сила огня»; одну из главных ролей в этом фильме сыграл Илай Уоллак, позднее появившийся в эпизодической роли в фильме «Таинственная река»; в этом же фильме снимался и Бэйкон.