Леонард Млодинов - Кратчайшая история времени

С 1887 по 1905 год было предпринято несколько попыток спасти теорию эфира. Наиболее известной из них была теория голландского физика Хендрика Лоренца, который попытался объяснить результат эксперимента Майкельсона и Морли, предположив, что при движении сквозь эфир объекты сокращаются в направлении движения, а ход часов замедляется. Но в своей знаменитой статье, опубликованной в 1905 году, никому тогда не известный клерк швейцарского патентного бюро Альберт Эйнштейн заметил, что необходимость в самой идее эфира отпадает, если отказаться от представления об абсолютном времени (вскоре станет ясно почему). Выдающийся французский математик Анри Пуанкаре высказал похожую идею за несколько недель до Эйнштейна. Но аргументы Эйнштейна оказались более физичными, чем соображения Пуанкаре, который рассматривал проблему с чисто математической точки зрения и до самой своей смерти не принял интерпретацию Эйнштейна.

Фундаментальным постулатом теории Эйнштейна, названной теорией относительности, было утверждение, что законы науки должны быть одинаковыми для любого движущегося наблюдателя независимо от его скорости. Это было справедливо и для законов движения Ньютона, но теперь Эйнштейн распространил эту идею и на теорию Максвелла. Другими словами, раз из теории Максвелла неизбежно вытекает постоянство скорости света, то измерения, выполненные любым движущимся равномерно и прямолинейно наблюдателем, должны дать одно и то же значение скорости света независимо от того, перемещается ли наблюдатель в направлении источника излучения или от него, и независимо от скорости движения наблюдателя. Это простая идея позволила объяснить – без привлечения какого-либо эфира или другой предпочтительной системы отсчета – смысл скорости света в уравнениях Максвелла, но при этом из нее вытекали и другие следствия, зачастую противоречащие нашим интуитивным представлениям.

Например, из одинаковости скорости света для всех наблюдателей следует необходимость изменения наших представлений о времени. Давайте снова представим себе несущийся на большой скорости поезд. Как мы уже установили в главе 4, с точки зрения играющего с мячиком для пинг-понга пассажиром путь мячика составил всего несколько десятков сантиметров, а с точки зрения наблюдателя на платформе этот же самый мячик преодолел расстояние около 40 метров. Точно так же если пассажир поезда посветит фонариком, то с точки зрения двух наблюдателей свет пройдет разные расстояния. Поскольку скорость равна расстоянию, деленному на время, то раз с точки зрения расстояния двух наблюдателей пройденные светом расстояния различаются, то единственный способ получить одинаковую скорость – это признать, что и промежутки времени между одной и той же парой событий различны для разных наблюдателей. Другими словами, в теории относительности нам придется расстаться с представлением об абсолютном времени! Теперь у каждого наблюдателя свое течение времени в соответствии с имеющимися при нем часами, и даже совершенно одинаковые часы у разных наблюдателей не обязаны отмерять одинаковое время между двумя событиями.

В теории относительности отпадает необходимость в эфире, присутствие которого, как показал эксперимент Майкельсона и Морли, невозможно обнаружить. Вместо этого теория относительности требует от нас фундаментального изменения наших представлений о пространстве и времени. Мы должны признать, что время не является чем-то совершенно отдельным от пространства, но образует с ним единое целое под названием пространство-время. Эти идеи не так то легко переварить. Физикам потребовалось несколько лет, чтобы окончательно признать теорию относительности. То, что Эйнштейн смог придумать такую теорию, свидетельствует о его потрясающем воображении. А то, что он смог делать из нее надлежащие выводы, несмотря на их кажущуюся противоречивость, свидетельствует о его уверенности в своих логических построениях.

Наш повседневный опыт говорит нам, что положение точки в пространстве можно писать тремя числами или координатами. Например, мы можем сказать о точке в комнате, что она расположена в семи метрах от одной стены, трех метрах от другой стены и на высоте пяти метров над полом. Или например, можно сказать, что некая точка расположена на определенной широте и долготе и на определенной высоте над уровнем моря. Мы можем использовать любые три подходящие координаты, хотя, конечно, в каждом конкретном случае их практическая применимость ограничена. Например, не очень-то удобно определять положение Луны, указав ее расстояние в километрах к северу и к западу от цирка Пикадилли и высоту в метрах над уровнем моря. Положение Луны лучше описывать через ее расстояния от Солнца и от плоскости орбит планет и угол между линией, соединяющей Луну и Солнце, и линией, соединяющей Солнце с ближайшей к нему звездой Проксима Центавра. Но такие координаты не очень годятся для описания положения Солнца в нашей Галактике или положения нашей Галактики в Местной группе галактик. В сущности, всю Вселенную можно описать как набор взаимно перекрывающихся областей, в каждой из которых можно использовать свою систему координат для определения положения заданной точки.

В теории относительности любое событие в пространстве-времени, то есть любое событие, которое происходит в определенной точке пространства в определенный момент времени, может быть описано четырьмя числами, или координатами. И в данном случае выбор координат также произволен: можно использовать любой набор из трех хорошо определенных пространственных координат и любой меры времени. Но теория относительности рассматривает пространственные и временные координаты как равноправные, так же как любые две пространственные координаты. Можно, например, выбрать новый набор координат, в котором, скажем, первая пространственная координата представляет собой некую комбинацию первой и второй пространственной координаты исходного набора. Так, вместо определения положения точки на Земле через ее расстояния к северу и западу от цирка Пикадилли в километрах можно использовать расстояния точки к северо-востоку и северо-западу от того же цирка Пикадилли. Точно так же мы можем перейти к использованию новой временной координаты, равной исходному времени (в секундах) плюс расстояние (в световых секундах) точки к северу от цирка Пикадилли.

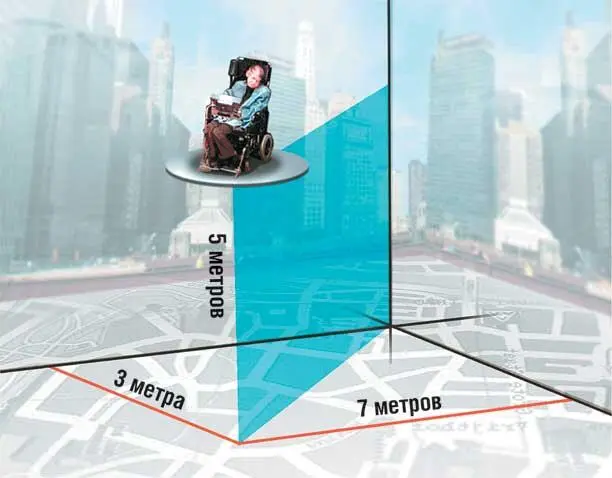
Координаты в пространстве. Когда говорят, что у пространства три измерения, то имеют в виду следующее: чтобы задать положение точки в нем, требуется три числа, или координаты. Если к этому описанию добавить время, то трехмерное пространство превращается в четырехмерное пространство-время