Дмитрий Поспелов - Моделирование рассуждений. Опыт анализа мыслительных актов

Чтобы все сказанное стало понятнее, рассмотрим конкретный пример. На рис. 26 показана серия изображений, соответствующая пропорции Лейбница, в которой, как всегда, надо восстановить недостающее звено, т.е. осуществить (если это возможно) вывод по аналогии. Для описания изображений введем язык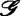и 1и 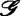2. В языке 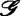1в качестве элементов возьмем изображение солнца s , и человечка m . В качестве отношений будем рассматривать отношения R 1– «быть слева вверху» и R 2– «быть справа вверху». Тогда ситуация А может быть описана как sR 1 m . В качестве операций в 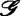1будем использовать перестановку объектов относительно друг друга O 1и вращение на 180° по часовой стрелке O 2. Тогда преобразование F можно описать как O 1( s , m ); O 2( m ). В результате этого возникает ситуация B , описание которой в языке 1выглядит как sR 2( O 2( m )).

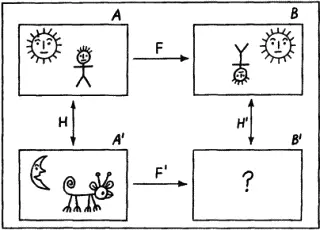
Рис. 26.

Введем теперь элементы языка 2. Это луна l и фантастическое животное q . В качестве отношений, используемых в 2, возьмем снова отношения R 1и R 2, а в качестве операций 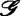2сохраним операции O 1и O 2языка 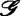1. Описание А’ выглядит следующим образом: lR 1 q . Для получения описания В’ установим между А и А’ отношение взаимно однозначного соответствия H , например, так, что имеют место взаимно однозначные соответствия s 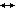l и m 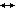q . Тогда sR 1 m 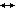lR 1 q и А 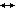А’ . Преобразование F’ в наших предположениях совпадает с F . Значит, В и В’ должны находиться также во взаимно однозначном соответствии. Но В есть sR 2( O 2( m )). Учитывая соответствие между элементам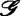и 1и 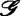2, выводим описание для В’ : lR 2( O 2( q )).

Рассмотренная процедура носит общий характер. Можно строго доказать, что если в пропорции Лейбница А , А’ и В описаны с помощью алгебраического языка, использующего лишь двуместные отношения, задан характер преобразований F и установлено взаимно однозначное соответствие между 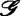1и 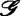2, то описание В’ также возможно на языке 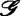2и существуют взаимно однозначные соответствия F 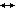F’ и В 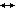В’ , так что, применяя к А преобразование F и к А’ преобразование F’ , получаем В и В’ , такие, что 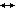В В’ .

Заметим, что из этого утверждения вытекает, что необходимым условием для возможности рассуждений по аналогии с использованием пропорции Лейбница служит требование коммутативности ее диаграммы. Требование коммутативности диаграммы означает, что описание В’ , полученное из A с помощью F и взаимно однозначного соответствия H’ , ничем не отличается от описания В’ , полученного из A с помощью взаимно однозначного соответствия H и последующего применения к этому результату преобразования F’ . С требованием коммутативности диаграмм мы еще столкнемся в последующих разделах этой главы.

Несмотря на все сказанное, полное описание модели рассуждений по аналогии всё еще не получено, так как пропорция Лейбница явно не исчерпывает всех случаев рассуждений подобного типа. Да и в случае, когда мы имеем дело действительно с пропорцией Лейбница, остаются нерешенными по крайней мере два вопроса: как построить язык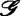и 1и 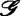2и как установить взаимно однозначное соответствие между ними. Возможные в этом случае трудности иллюстрирует рис. 27. На этом рисунке показаны ситуации А и А’ . Ситуация А может быть описана следующим текстом: «Ромео любит Джульетту. Джульетта любит Ромео (на рис. 27 это отношение R 1). Ромео мужчина ( R 2). Он итальянец ( R 3). Джульетта женщина ( R 4). Она красива ( R 5). Она не замужем ( R 6)». Ситуация А’ может быть описана следующим текстом: «Тристан любит Изольду. Изольда любит Тристана ( R 1). Тристан мужчина ( R 2). Он бретонец ( R * 2). Изольда женщина ( R 4). Она красива ( R 5). Она замужем ( R * 6). Ее муж – король Марк ( R 7)».

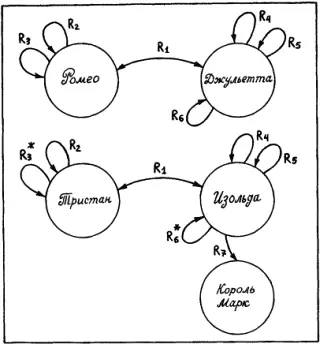
Рис. 27.

Готовы ли мы признать описанные две ситуации аналогичными? И должен ли Тристан действовать так же, как Ромео? Из соответствующих литературных произведений мы знаем, что развитие ситуации А было таково, что оно привело к совместной смерти Ромео и Джульетты. А Тристан и Изольда имели другую судьбу. Почему это произошло? И можно было бы это формально установить в процессе сравнения ситуаций А и А’ ? Ведь во второй ситуации имелся король Марк, а различное число отношений заведомо не позволяло установить взаимно однозначное отношение между их описаниями. Но может быть вместо изоморфизма (т.е. взаимно однозначного отношения) для 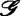1и 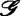2достаточно какого-нибудь гомоморфизма?

Этот вопрос пока остается без ответа. Поэтому ограничимся лишь тем, что для рассуждений по аналогии можно считать твердо установленным. В следующем разделе попытаемся объединить то, что нам уже известно об индуктивном методе Милля и рассуждениях по аналогии.

Сокращение ДСМ, вынесенное в название метода, означает Джон Стюарт Милль. Оно показывает, что метод поиска закономерностей по множествам положительных и отрицательных примеров, к описанию которого мы переходим, опирается на методы индукции, предложенные этим ученым. Их реализация в виде комплекса действующих программ на ЭВМ выполнена современными исследователями.