Джеймс Гордон - Почему мы не проваливаемся сквозь пол

Обратимся теперь к рис. 31 и 32, на которых изображены действительные картины напряжений, рассчитанные для трещины длиной 2 мкм и радиусом кончика 1А. Часть трещины, прилегающая к ее кончику, отмечена на рисунке штриховкой. Кривые линии проходят через точки тела, в которых коэффициент концентрации остается постоянным для напряжении, направленных по вертикали (рис. 31) и по горизонтали (рис. 32) в плоскости листа. (Заметьте, это - не траектории напряжений!) Число у каждой линии обозначает величину коэффициента концентрации, то есть число К , на которое следует умножить величину среднего напряжения на значительном удалении от трещины, чтобы получить соответствующее напряжение в любой точке на заданной линии. Когда размер трещины увеличивается, радиус ее кончика не изменяется; следовательно, концентрация напряжений возрастает. Но характер распределения напряжений остается прежним, все изменяется пропорционально. Для случая, когда трещина укорачивается, справедливо, конечно, обратное.

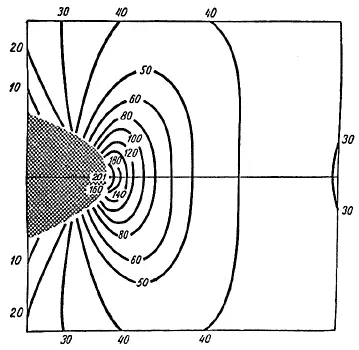
Рис. 31. Концентрация напряжении вблизи кончика эллиптической трещины.

Растягивающие напряжения направлены под прямым углом к трещине, то есть параллельно приложенной нагрузке. Заштрихованная область представляет собой трещину. Вдоль кривых коэффициенты концентрации постоянны, числа, проставленные на них, показывают, таким образом, во сколько раз местное напряжение превышает среднее по образцу. Максимальная величина концентрации - около 200. Абсолютная величина концентрации зависит от длины трещины, но пропорции остаются неизменными.

Из рис. 31 видно, что напряжения, направленные вертикально, то есть силы, стремящиеся раскрыть трещину, разорвать ее, очень велики, особенно в области, вплотную примыкающей к кончику трещины. Самые опасные напряжения приходятся на область, примерно равную площади одной атомной связи. Численная величина максимального напряжения равна здесь полученному Инглисом напряжению в самой крайней точке трещины (правда, это точное значение не столь уж важно, потому что все подобные расчеты основаны на каких-то допущениях). Но если мы продвинемся вперед от трещины, перескочим, грубо говоря, на следующую атомную связь, то обнаружим, что напряжение на ней упало в два с лишним раза по сравнению с максимальной величиной. Вероятно, эти соотношения верны всегда, и они очень ясно показывают, что большая часть нагрузки концентрируется в материале на единственной цепочке атомных связей, проходящей через самый кончик острой трещины; следует лишь помнить, что мы имеем дело с твердым телом (а не с листом бумаги) и кончик трещины представляет собой линию в трехмерном пространстве. Как только перегруженная связь на кончике трещины лопнет, пик концентрации напряжений переместится на следующую связь и т.д. и т.д., подобно петлям на чулке.

Если увеличивать только прочность химических связей, то это мало повлияет на прочность тела, содержащего дефекты, так как этот путь не уменьшает концентрации напряжений у трещин. Именно поэтому алмаз и сапфир - вещества хрупкие и обычно не очень прочные, несмотря на их большую твердость и высокую энергию химических связей. На этом можно было бы и поставить точку в истории о прочности и хрупкости, если бы дело ограничивалось более или менее упругими и более или менее однородными телами. С такой точки зрения практически безразлично, с какого рода телом мы имеем дело - кристаллическим, стеклообразным или даже полимером; несущественна и величина модуля Юнга. Важно лишь, чтобы тело подчинялось закону Гука в достаточно широкой области деформаций, вплоть до разрушения. Хрупкость - не есть особое состояние, она является нормальным состоянием всех простых твердых тел.

Вязкость присуща более сложному твердому телу; можно даже сказать, что тело должно быть специально “сконструировано” таким образом, чтобы обладать этим свойством. Вязкие материалы часто содержат в своем объеме какие-то границы раздела, многие из этих материалов - тела неоднородные, то есть построены из двух или более составляющих, например из волокна и смолы.

Давайте теперь рассмотрим рис. 32, на котором изображена картина напряжений, параллельных трещине и направленных горизонтально. Сразу и не подумаешь о том, что такие напряжения, и довольно значительной величины, существуют, однако более внимательный анализ показывает, что дело обстоит именно так. Как видно из рис. 30, все траектории напряжений должны обходить край трещины, довольно резко изгибаясь при этом. Траектории напряжений можно образно представить себе в виде натянутых струн, которые стремятся выпрямиться. Если натянутая струна огибает жесткий колышек, она будет давить на колышек в направлении натяжения, а реакция колышка, естественно, будет направлена в противоположную сторону. Иными словами, в области, примыкающей к трещине со стороны ее кончика, должно существовать растяжение в направлении, параллельном поверхности трещины. Вычисления Кука дают распределение и величину соответствующих напряжений (рис. 32).

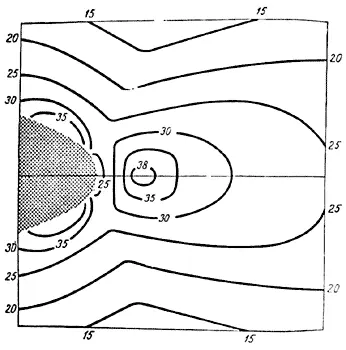
Рис. 32. Концентрация напряжении вблизи кончика эллиптической трещины. Растягивающие напряжения направлены параллельно трещине, то есть под прямым углом к направлению приложенной нагрузки. Для этого случая максимальная концентрация составляет около 40 - т.е. пятую часть концентрации, показанной на предыдущем рисунке.

Если напряжения, перпендикулярные трещине, достигают максимума на самом се кончике, то напряжение, параллельное трещине (горизонтальное в плоскости чертежа), равно нулю в этой точке. Оно увеличивается с удалением от кончика по горизонтали (рис. 32) и достигает максимума на расстоянии одного-двух атомных размеров от трещины. Но этот максимум размазан, и довольно высокие напряжения сохраняются на значительном расстоянии от трещины. Независимо от формы трещины и способа ее погружения отношение максимальной величины напряжения, параллельного трещине, к максимальной величине напряжения, направленного перпендикулярно ее поверхности, есть величина постоянная и равная приблизительно 1/5.Такое положение имеет, по-видимому, фундаментальное значение для всех трещин, существующих в растянутом материале.

Здесь-то и становятся важными внутренние поверхности в биологических материалах. Важно то, что эти поверхности раздела обычно слабее окружающего их материала И не потому, что Природа не догадалась склеить здесь ткани попрочнее, а потому, что, будучи верно устроенными, слабые поверхности делают материал вязким, упрочняют его.