Борис Штерн - Прорыв за край мира

Через десятилетия люди запускают космический аппарат с прецизионным приемником микроволнового радиоизлучения, испущенного миллиарды лет назад. И видят из карты этого излучения ту самую осциллирующую кривую!

Сахаров не дожил до этого момента, и Зельдович не дожил. Но Рашид Сюняев и другие, исследовавшие этот эффект в более реалистичной постановке задачи, дожили. Думаю, лучшей награды за теоретическую научную работу не придумать.

Как увидеть акустические стоячие волны, точнее, осцилляции их амплитуды? Надо подвергнуть их гармоническому анализу, иными словами, разложить на мультиполи и посмотреть, как ведут себя коэффициенты разложения. Что такое мультиполи? Самый малый — это диполь ( l = 1). Диполь показывает разницу в более яркой и менее яркой половинах неба. При этом основной вклад в диполь дает движение Солнечной системы вместе с Галактикой относительно усредненной системы покоя Вселенной — эта скорость около 600 км/с. Там, куда мы движемся, реликтовое излучение кажется ярче, а там, откуда движемся — слабее. Отделить диполь, связанный с аберрацией от нашего движения, от истинного диполя реликтового излучения невозможно, поэтому он просто выбрасывается из анализа. Следующий — квадруполь ( l = 2), он отражает глобальную сплюснутость (или вытянутость) распределения яркости. И т. д.

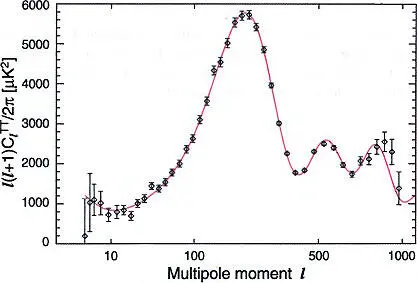
Рис. 32.1. Разложение карты реликтового излучения, снятой WMAP за 9 лет наблюдений, по угловым мультиполям (спектр мощности). Традиционно изображают величину l (l+ 1) C l . Из статьи G. Hinshaw et al. arXiv:1212.5226

Двумерное разложение сферической карты отличается от одномерного разложения Фурье тем, что каждый мультиполь l представлен суммой 2 l + 1 членов со своими коэффициентами. Для того, чтобы увидеть, какие масштабы неоднородностей сильнее выражены, все эти коэффициенты не нужны — достаточно взять среднее от суммы их квадратов (традиционно обозначаемое как С l ). Соответствующее распределение называется спектром мощности, именно оно показано на рис. 32.1.

Высокий пик слева означает, что карта имеет самую контрастную пятнистость при размере пятна около градуса. Он соответствует акустическим волнам, пришедшим к моменту рекомбинации с фазой π . За одно колебание они успели подрасти из-за гравитационного взаимодействия с темной материей, которая за это время «скомковалась» в сто раз сильней барионного вещества. Правее — следующие пики, соответствующие фазам 2 π , 3 π и т.д. Пики при увеличении номера мультиполя (уменьшении размеров неоднородностей) становятся ниже, потому что оказываются «замытыми» из-за диффузии фотонов, которые успевают частично разбежаться из сгущения вещества за период колебания стоячей волны. Это так называемый эффект Силка. Особенно хорошо этот эффект наблюдается на рис. 32.2, где тот же самый спектр мощности дан в логарифмическом масштабе и к нему добавлены данные наземных установок с меньшим охватом неба, но с лучшим угловым разрешением.

Черные точки с ошибками (те же, что и на рис. 32.1) — результат WMAP. Голубые точки — результат обзора небольшой части неба, сделанного с лучшим угловым разрешением с помощью микроволнового телескопа на Южном полюсе (SPT). Оранжевые точки — данные Космологического телескопа в Атакаме (ACT). Сплошная кривая — результат подгонки теории только к данным WMAP, данные при муль-типольных моментах больше тысячи не использовались!

Точки с наименьшими ошибками получены на микроволновом телескопе, расположенном на Южном полюсе (тарелка диаметром Юм) — там фон от теплового излучения атмосферы меньше, чем в не столь экстремальных местах.

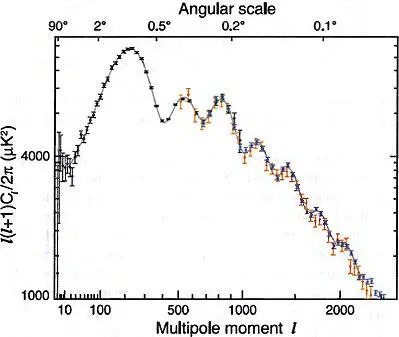
Рис. 32.2. То же самое разложение, что и на рис. 32.1, но в логарифмическом масштабе и с добавлением данных наземных микроволновых телескопов (см.текст). Из статьи G. Hinshaw et al. arXiv:1212.5226

Осциллирующая кривая на рис. 32.2 поразительно информативна. Это примерно тоже самое, как если бы мы увидели на карте ранней Вселенной масштабную линейку с делениями в мегапарсеках, да и не только линейку — целую метеостанцию с различимыми показаниями на циферблатах. Причем эти показания точнее, чем можно извлечь из параметров современной Вселенной. В частности, положение пиков весьма чувствительно к кривизне Вселенной Ω k — этот параметр примерно равен относительному отклонению суммы углов треугольника от 180°, если треугольник имеет размер с видимую часть Вселенной (вспомним надуваемый шарик на лекции С. П. Капицы — кривизна его поверхности дает наглядную аналогию). Оказывается, наша Вселенная с хорошей точностью «плоская» на масштабе горизонта ( Ω k = -0,037 ± 0,043, если брать только данные WMAP и Ω k = 0,001 ± 0,012, если привлечь также данные наземных микроволновых телескопов). Высота пиков чувствительна к относительного му вкладу барионов в содержимое Вселенной. Соотношение между вторым и третьим пиками зависит от вклада темной материи. И т. д.

Конечно, эффекты от всех этих и других параметров запутаны, и их извлекают не по отдельности, а все вместе посредством процедуры, называемой «подгонкой методом максимального правдоподобия». Для подгонки кроме данных нужна теоретическая модель, которая должна описать данные. В этом случае она слишком сложна, чтобы ее можно было выразить формулой. Модель включает в себя все процессы, о которых шла речь выше. Прежде всего это генерация начального спектра неоднородностей.

Мы писали о том, что относительная амплитуда начальных неоднородностей должна быть порядка 5·10 -5, а их спектр — плоским. На самом деле мы не знаем точно ни того, ни другого. Поэтому амплитуда берется за один из подгоночных параметров. Спектр неоднородностей не обязан быть в точности плоским, даже если мы уверены, что источником неоднородностей является механизм космологической инфляции. Дело в том, что в процессе инфляции величина ответственного за нее поля хоть и медленно, но меняется — это дает спектру небольшой наклон, который тоже входит в число подгоночных (свободных) параметров. Далее концентрация обычного (барионного) вещества влияет на высоту пиков и соотношение между ними. Это третий свободный параметр. Темная материя дает неоднородный гравитационный потенциал, влияющий на акустические волны. Ее концентрация — четвертый свободный параметр. Далее — кривизна Вселенной, пятый параметр. От него будет зависеть угол, под которым мы видим пятно определенного размера и, следовательно, положение всех пиков. Похожий эффект дает темная энергия, от нее зависит время распространения фотонов после рекомбинации и, соответственно, расстояние, которое они пролетели. Так что плотность темной энергии — это еще один параметр. Правда, не все эти параметры независимы: полная плотность энергии во Вселенной в сумме с вкладом кривизны, пропорциональным Ω k , должна давать критическую плотность. Так что пока свободных параметров пять.