Джон Дрейер - История астрономии. Великие открытия с древности до Средневековья

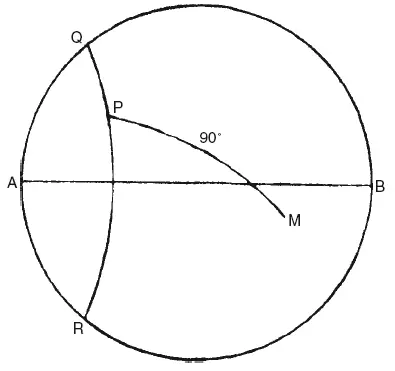
На поверхности третьей сферы зафиксированы полюса четвертой, причем ее ось постоянно наклонена на свою величину для каждой планеты относительно оси третьей сферы. Четвертая сфера вращается вокруг своей оси за тот же период, но в направлении противоположном направлению вращения третьей сферы. На экваторе четвертой сферы закреплена планета и, таким образом, наделена четырьмя движениями: одним суточным, другим орбитальным по зодиакальному кругу и еще двумя в синодический период. Какое действие оказывают эти два последних движения на видимое положение планеты в небе? На приводимом рисунке сфера (третья) вращается вокруг фиксированного диаметра АВ (мы можем вообще не учитывать движение первой, суточной, сферы, и покамест пренебречь и движением второй сферы); во время этого вращения вокруг АВ некоторая точка Р, один из полюсов четвертой сферы, описывает небольшой круг QPR , в то время как эта четвертая сфера в тот же период, но в противоположном направлении, завершает вращение вокруг Р и другого полюса Р′. Планета находится в точке М на экваторе четвертой сферы, таким образом РМ= 90°. Следующая задача заключается в том, чтобы определить путь, описываемый М, спроецированный на плоскость окружности AQBR. Это довольно просто сделать при помощи современной математики, но мог ли Евдокс решить эту задачу при помощи простых геометрических рассуждений? Этот вопрос превосходно исследовал Скиапарелли и показал, что решение этой задачи было по силам геометру такого несомненного таланта, как Евдокс. В итоге получается, что проецируемый путь симметричен относительно линии АВ , что на ней есть двойная точка и что это не более чем всем известная «восьмерка», или лемниската, уравнение которой: г 2= а 2 cos 2θ, или, строго говоря, фигура такого рода, лежащая на поверхности небесной сферы, по каковой причине Скиапарелли называет ее сферической лемнискатой. Продольная ось кривой проходит вдоль зодиака, а ее длина равна диаметру окружности, описываемой Р, полюсом сферы, которая несет планеты. Двойная точка находится в 90° от двух полюсов вращения третьей сферы. Планета описывает кривую, двигаясь в направлении, указанном стрелкой, и проходит дуги 1—2, 2—3, 3—4, 4—5 и т. д. за равные промежутки времени.

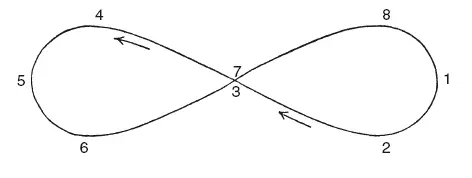
До сих пор мы рассматривали только движение точки М под действием вращений третьей и четвертой сферы. Но сейчас мы должны вспомнить, что ось АВ обращается вокруг эклиптики в течение сидерического периода планеты. Во время этого движения продольная ось лемнискаты всегда совпадает с эклиптикой, по которой кривая движется с одинаковой скоростью. Поэтому для третьей и четвертой сферы мы можем заменить лемнискату, по которой планета движется вышеописанным образом. Сочетание этого движения с движением кривой по эклиптике дает видимое движение планеты через созвездия. Движение планеты по лемнискате состоит в колебании вперед и назад, причем период равен синодическому периоду обращения, и в первой половине этого периода движение планеты по эклиптике ускоряется, а во второй половине – замедляется, когда два движения совершаются в противоположных направлениях. Поэтому, когда на дуге лемнискаты обратное колебание происходит быстрее, чем одновременное движение вперед самой лемнискаты, планета какое-то время движется в обратную сторону, до и после чего она некоторое время находится в неподвижном состоянии, пока оба движения уравновешивают друг друга. Очевидно, что наибольшее ускорение и наибольшее замедление имеют место, когда планета проходит через двойную точку лемнискаты. Таким образом, движения должны быть настолько сложны, что планета проходит через эту точку при поступательном движении во время верхнего соединения с Солнцем, где видимая скорость планеты по долготе наибольшая, тогда как она снова должна быть в двойной точке, но двигаться в обратном направлении во время противостояния или нижнего соединения, когда видимая скорость планеты при попятном движении максимальна. Такое сочетание движений, конечно, должно сопровождаться определенной долей движения по широте в зависимости от ширины лемнискаты.

Эту кривую греки называли гиппопедой (ἵππου πέδδη), потому что это было излюбленное упражнение в школе верховой езды – заставить галопирующую лошадь описывать такую фигуру, и Симпликий в своем изложении планетарной теории Евдокса прямо говорит, что планета описывает кривую, которую Евдокс именует гиппопедой. Это слово встречается несколько раз в комментарии Прокла к первой книге Евклида, где описываются плоские сечения твердого тела, полученные обращением круга вокруг прямой линии в его плоскости, при условии, что линия не пересекает круга. Сечение, образованное плоскостью, параллельной этой линии и касающейся внутренней поверхности тора, Прокл называет гиппопедой, и, следовательно, мы имеем доказательство, что Евдокс и его последователи имели четкое представление о свойствах кривой, получающейся в результате движения третьей и четвертой сферы. О кривой и ее применении говорит Теон Смирнский (с. 328), описывая астрономическую теорию платоника Деркиллида: «Он полагает, что в спиральных линиях и тех, что похожи на конные упражнения, не надо видеть причину блужданий планет, так как эти линии получаются случайно [87], однако главная причина блужданий и спиралей заключается в наклонном движении по зодиакальному кругу». Далее Теон говорит о видимой спирали, которую описывает планета, в духе платоновского «Тимея»; но отвергаемое Деркиллидом мнение – это, вне всяких сомнений, именно то движение по лемнискате, которое изобрел Евдокс.

Если теперь мы спросим, насколько эту теорию можно согласовать с реально наблюдаемыми движениями светил, то нам прежде всего нужно вспомнить, что мы не знаем, производил ли Евдокс какие-либо наблюдения с целью установить величину ретроградных движений, или ему просто было известно, что такие движения существуют, хоть он и не располагал никакими соответствующими числовыми данными. Чтобы проверить теорию, нам требуется знать сидерический период, синодический период и расстояние между полюсами третьей и четвертой сферы, которое Скиапарелли называет наклонением. Величину этого расстояния, определенную Евдоксом для каждой планеты, не указывает ни Аристотель, ни Симпликий, а периоды приводит лишь Симпликий в округленных числах (с. 496):