Николай Кондратьев - Ориентировка по звездам

h + z = 90°.

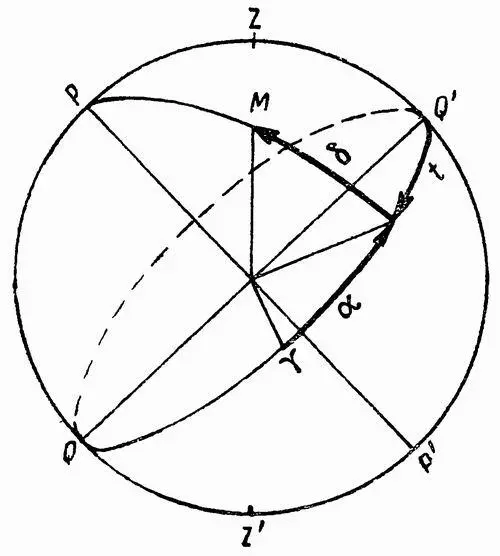
Рис. 10. Экваториальная система координат

Зенитные расстояния отсчитываются также по дуге вертикала, но только от зенита. Они могут иметь значения от 0° до 180°. Светила, расположенные в подгоризонтной части небосвода, имеют зенитное расстояние более 90°.

Экваториальная система координат (рис. 10). В этой системе координат основными кругами, относительно которых определяется место светила, являются небесный экватор и небесный меридиан. Положение светила определяется часовым углом (t) и склонением (δ). Часовым углом светила называется угол, отсчитываемый по дуге небесного экватора от южной части небесного меридиана до круга склонения светила. Он отсчитывается В западном и восточном направлениях от 0 до 180° и соответственно обозначается: западный часовой угол — t З, восточный часовой угол — t B.

Склонением светила называется угол, отсчитываемый по дуге круга склонения от небесного экватора до светила, т. е. угол между плоскостью небесного экватора и направлением на светило. Склонение может иметь значения от 0° до ±90°. Если светило находится в северной полусфере, его склонение считается положительным, если в южной — отрицательным.

Вместо часового угла иногда пользуются другой координатой— прямым восхождением светила (а), которое в отличие от часового угла является постоянным и не изменяется со временем, так как не зависит от вращения небесной сферы.

Поясним геометрический смысл этой координаты. Положение Солнца относительно звезд меняется. В течение года Солнце описывает полный круг на небесной сфере, за это время дважды — весной и осенью — пересекая небесный экватор. Точка небесного экватора, через которую центр Солнца проходит весной (21 марта), называется точкой весеннего равноденствия и обозначается знаком ¡ (знак созвездия Овна). Прямое восхождение светила — это угол, отсчитываемый по небесному экватору от точки весеннего равноденствия до круга склонения светила. Прямое восхождение измеряется от 0° до 360° против хода часовой стрелки, если смотреть с северного полюса мира, т. е. навстречу суточному вращению небесной сферы.

Основное достоинство горизонтной системы заключается в простоте измерения координат. По азимуту и высоте светила, измеренным в полете, путем расчетов можно определить местонахождение наблюдателя, курс самолета и время.

Однако знания только горизонтных координат светил недостаточно для решения других задач. Кроме того, горизонтные координаты с течением времени непрерывно и неравномерно изменяются (вследствие вращения небесной сферы) и зависят от местонахождения наблюдателя на Земле, которое обусловливает положение плоскости истинного горизонта.

В противоположность этому положение небесного экватора на небесной сфере не зависит от времени и места наблюдателя на Земле, следовательно, склонение каждого светила, отсчитываемое от экватора, — величина постоянная. Прямое восхождение, которое отсчитывается от точки весеннего равноденствия, вращающейся вместе с небесной сферой, тоже постоянно для каждого светила. Часовой угол вследствие равномерного вращения небесной сферы изменяется с течением времени равномерно. Поэтому карты неба и астрономические ежегодники составляются в экваториальных координатах.

Горизонтные и экваториальные координаты светил связаны между собой определенными соотношениями.

Интересно отметить, что широта места наблюдателя равна высоте полюса мира (φ набл= h п.м), потому что стороны углов взаимно перпендикулярны (рис. 11). Так будет в любой точке земного шара. В этом легко убедиться, наблюдая Полярную звезду, которая расположена близ полюса мира, из различных мест, значительно удаленных друг от друга по широте. Даже невооруженным глазом можно определить, что Полярная звезда в Москве (φ ≈ 56°) выше, чем в Краснодаре (φ ≈ 45°), а в Архангельске (φ ≈ 64°) выше, чем в Москве. На Северном географическом полюсе (φ = 90°) Полярная звезда расположена прямо над головой, в зените.

Таким образом, измерив высоту полюса мира (практически высоту Полярной звезды), наблюдатель получит географическую широту своего места.

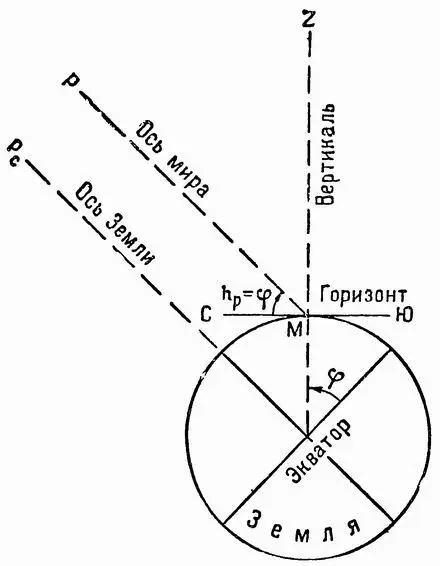
Рис. 11. Высота полюса мира равна географической широте места наблюдателя

Каждое светило в своем суточном движении вокруг оси мира пересекает небесный меридиан в двух точках. Момент прохождения светила через небесный меридиан называется кульминацией светила. Различают верхнюю и нижнюю кульминации. При верхней кульминации высота светила наибольшая, а при нижней — наименьшая. В северной полусфере азимут светила в момент верхней кульминации равен 180°, а в момент нижней —0°. Исключением являются азимуты незаходящих светил, верхние кульминации которых происходят между полюсом и зенитом. У этих светил азимуты при верхней и нижней кульминациях равны 0°.

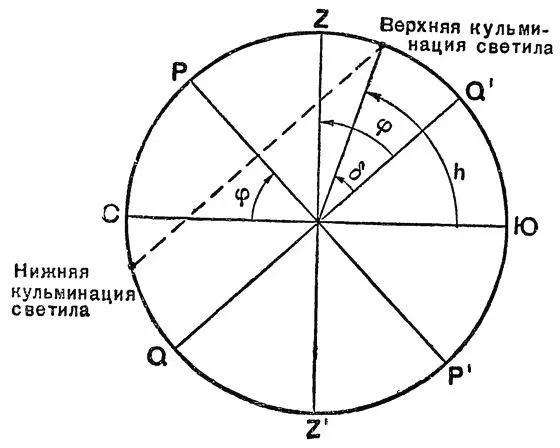
Рис. 12. Соотношение между высотой и склонением светила в момент кульминации и широтой места наблюдателя

Весьма важным является соотношение между широтой места наблюдателя φ, склонением δ и высотой h светила в момент его кульминации. На рис. 12 показано светило в верхней кульминации между точкой юга и зенитом. Из рисунка видно, что в этом случае

h = 90° — φ + δ.

Если светило в верхней кульминации находится между зенитом и полюсом, то

H = 90° + φ —δ.

Рассуждая таким же образом, для нижней кульминации светила получим

h = φ + δ — 90°.

По этим соотношениям, зная широту местонахождения наблюдателя (определяется по карте) и склонение светила (находится по «Астрономическому ежегоднику»), можно рассчитать высоту светила в момент кульминации и, сравнив ее с фактически измеренной высотой в момент кульминации, вычислить поправку секстанта. По высоте светила, измеренной в момент кульминации, можно рассчитать также широту своего местонахождения.

В ясную безлунную ночь над нашей головой видны и яркие звезды, сразу привлекающие к себе внимание, и менее яркие, и еле различимые невооруженным глазом. В одной стороне неба одни звездные рисунки, в другой — другие (см. приложение). Некоторые группы звезд своими рисунками напоминают какие-то фигуры: ковша, креста, серпа и т. д.

Наиболее яркие звезды отличаются друг от друга и цветом. Из-за различия температуры поверхности звезд одни из них излучают белый свет, другие — желтоватый, третьи— красноватый или оранжевый и т. д.