Рудольф Юбельт - Определитель минералов
- Название:Определитель минералов
- Автор:
- Жанр:
- Издательство:ИЗДАТЕЛЬСТВО «МИР»
- Год:1978
- Город:Москва
- ISBN:нет данных
- Рейтинг:
- Избранное:Добавить в избранное
-
Отзывы:
-
Ваша оценка:
Рудольф Юбельт - Определитель минералов краткое содержание
Вторая книга из серии определителей геологических объектов, выпускаемой в ГДР (первая — «Определитель горных пород» — в русском переводе вышла в издательстве «Мир» в 1977 г.). Книга содержит краткие сведения по минералогии и кристаллографии, дает представление о внутреннем строении Земли, ее составе. Описание 205 главнейших природных минералов, в том числе рудных, составлено по единой схеме и сопровождается диагностическими таблицами.
Четкий и легкодоступный для понимания язык книги делает ее ценной не только для геологов всех специальностей, но также для массового читателя — туристов, школьников старших классов, студентов и всех любителей камня.
Определитель минералов - читать онлайн бесплатно полную версию (весь текст целиком)
Интервал:
Закладка:
Примеры: 432 — кубическая, 422 — тетрагональная, или 23 — кубическая, 32 — тригональная.
Следует, однако, показать яснее, что кристаллографические сингонии определяются непосредственно симметрией кристаллов. Наличие тетрагональной оси симметрии предопределяет условие а=b, угол между этими осями равен 90°. Ведь если вращение на 90° должно привести к идентичной картине, необходимо, чтобы отрезки по обеим осям были одинаковы. Аналогичные соотношения имеют место в гексагональной сингонии. В кубической сингонии соответственно три двойные или четверные оси симметрии связаны с четырьмя тройными осями, располагающимися вдоль пространственных диагоналей куба; обе системы осей пересекаются под характеристическим углом 54°44′.
Следует поставить важный вопрос, обсуждение которого еще более прояснит соотношения между сингонией, классом симметрии и элементом симметрии. Расположены ли элементы симметрии в кристалле произвольно или и здесь выявляются закономерные соответствия? Оказывается, что элементы симметрии тесно связаны с кристаллографическими осями. Для отдельных сингонии установлены следующие главные направления (параллельные лучу зрения):
| Сингония | Главные направления |
| Триклинная | Отсутствуют |
| Моноклинная | Ось b |
| Ромбическая | Ось а, ось b, ось с |
| Тетрагональная Гексагональная (Тригональная) | Ось с, оси а, биссектриса угла между осями а |
| Кубическая | Оси а, пространственные диагонали куба, диагонали граней куба |
Главными направлениями в кристалле называются направления, в которых располагаются элементы симметрии. Отсюда следует, что элементы симметрии могут находиться только в строго определенных направлениях.
В триклинной сингонии главное направление не установлено, поскольку придавать направление оси идентичности 1 или 1, т. е. точке, было бы бессмысленно. В моноклинной сингонии достаточно одного направления и для класса 2/m, поскольку эта комбинация оси и плоскости располагается в кристалле таким образом, что нормаль (перпендикуляр) к двойной оси ориентирована параллельно плоскости симметрии. Для других сингонии необходимо указывать три главных направления, хотя в кристаллах этих сингонии может присутствовать большое количество направлений, но два или даже три из них являются равноценными (например, в тетрагональной сингонии а=b или в кубической а = b = с), так что указание одного из таких направлений включает в себя и остальные, ему адекватные.
Поскольку каждый класс симметрии подчиняется какой–либо одной сингонии, с помощью главных направлений определяется положение элементов симметрии в пространстве. Само собой разумеется, что существует и обратная связь, в соответствии с которой кристаллографическим осям отвечают определенные элементы симметрии. Примеры:
| Класс симметрии | Сингония | Положение элементов симметрии |
| 2/m | Моноклинная | 2 || b m_ |_ b |
| 2/m 2/m 2/m | Ромбическая | 2 || а 2 ||b 2 || с |
| 4/m 2/m 2/m | Тетрагональная | т _ |_ a m_ |_ b m_ |_ с 4 || с 2 || а, b 2 || биссектрисам углов между осями а m_ |_ c т_ |_ a, b m _ |_ биссектрисам углов между осями а |
| 6 | Гексагональная | 6||с |
| 432 | Кубическая | 4||а, b , с 3 || четырем пространственным диагоналям куба 2 || шести диагоналям граней куба |
|| —параллельно
_ |_ — перпендикулярно
Пример класса 6 показывает, что не в каждом классе симметрии все главные направления соответствующей сиигонии сопровождаются элементами симметрии.
Внешнюю огранку кристаллов составляют грани, ребра и углы, которые связаны между собой соотношением Эйлера: число граней+число углов=число ребер +2.
Подобно элементам симметрии следует привести также грани и ребра кристаллов в соответствие с кристаллографическими осями и тем самым с элементами симметрии.
Легко представить, что каждая грань, рассматриваемая в пространстве, заключенном в систему координатных осей, должна отсекать, пересекать одну, две или три оси. Различают ряд положений граней, представленных на рис. 6.
Ребра кристаллов также обозначаются тройным индексом: ось а и все параллельные ей ребра имеют индекс [100], ось b — [ 010] и ось с — [ 001].
Общий символ грани, пересекающей все три оси, — ( hkl), ребра — [ uvw]. Обратите внимание на различную форму скобок!
Необходимо упомянуть еще одну особенность. Если грань отсекает на оси а одну часть, на оси b — две части и располагается параллельно оси с, то ее индекс будет не (120), а (210). Для индицирования граней, согласно Миллеру, применяются обратные значения для длин отрезков по осям. Грань отсекает отрезки a, b и с в отношении 1: 2: оо. Обратные значения составляют 1/1: 1/2:1/оо, а приведенные к целым числам — (210).
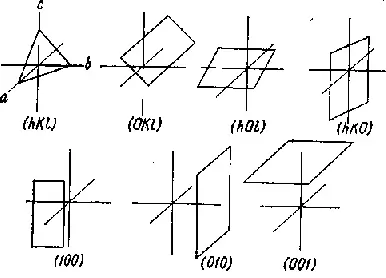 Рис. 6.
Рис. 6. 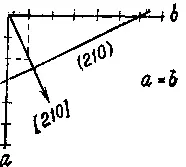 Рис. 7.
Рис. 7.
Для индицирования ребер, наоборот, используется прямое отношение отрезков. Благодаря применению обратных и прямых отрезков достигается одинаковое написание индексов для некоторых граней и нормалей к ним (рис. 7).
Для грани в общем положении принимается индекс (hkl), а для соответствующих ребер — [uvw]. Какие числа скрываются за этими буквенными обозначениями? Это малые числа (целые), часто 1 и 0, реже 2. Числа больше 2 почти не появляются в обозначениях индексов праней и ребер. Тот факт, что длины отрезков, отсекаемых гранями или ребрами на трех основных осях [Отрезки, отсекаемые гранью по кристаллографическим осям, в отечественной литературе принято называть параметрами этой грани. — Прим. перев. ], относятся между собой как малые целые рациональные числа, носит название в кристаллографии закона рациональности отношений параметров. Необходимо подчеркнуть, что абсолютные значения величин, между которыми определяют отношения, не во всех случаях одинаковы. Для ромбической сингонии а=/=b=/=с. Это означает для грани (111) ромбического кристалла различные абсолютные значения отрезка, отсекаемого по каждой оси, но равное количество этих отрезков по а, Ь и с. Так что получается отношение 1 а:1b:1с. По равенству или неравенству величин или длин отрезков по a, b и с определяют кристаллографические сингонии.
Прямое отношение а: b: с, упрощенно а: 1: с, обозначается как геометрическое осевое отношение. В кубической сингонии оно составляет, естественно, 1: 1: 1, в тетрагональной и гексагональной 1: 1: с, а начиная с ромбической и в сингониях с более низкой симметрией — а: 1: с. Осевое отношение является константой вещества. Если мы знаем это отношение и установили, что оно равно таковому известного минерала, тогда с полной уверенностью можно говорить об идентичности обои: минералов.
Читать дальшеИнтервал:
Закладка:








