Рудольф Юбельт - Определитель минералов

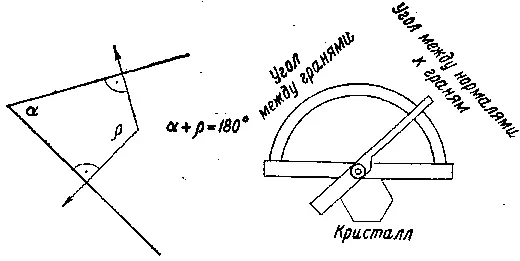
Рис. 8.

В заключение следует познакомить любителей минералов с методом, который позволяет во многих случаях более точно диагностировать минералы, но о котором, однако, в большинстве определителей минералов не упоминается. В описаниях минералов в данной книге наряду с сингонией приведены также класс симметрии и геометрическое осевое отношение, что облегчает возможность сравнения. Если минералы встречаются в искаженных формах, то сингония и тем более класс симметрии определяются лишь с трудом. Но искажение не затрагивает углов между кристаллографическими гранями. Углы между одинаковыми гранями кристалл–всегда одинаковы. Установлением этого закона постоянства углов Стеной в 1669 г. заложил основы кристалле графин. Углы между кристаллографическими гранями измеряются гониометром. Следует различать гранные углы и углы между нормалями к граням. Первые дополняют вторые до 180°. С помощью простого прикладного гониометра, который легко изготовить из транспортира и полоски картона, при аккуратной работе могут быть измерены углы с точностью до ±1°. Соответствующие грани минерала крепко зажимают между транспортиром и картонной линейкой (рис. 8) и считывают значение угла между нормалями и гранями. Необходимо учитывать, что последующие вычисления действительны только для углов между нормалями к граням.

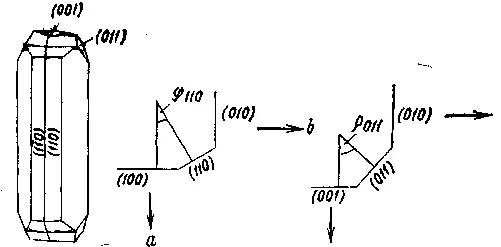
Рис. 9.

Что вообще подлежит вычислению? Не что иное, как геометрический индекс минерала — его осевое отношение а: 1: с. Согласно закону рациональности отношений параметров, у кристалла следует ожидать наличия граней с малыми индексами. Углы между нормалями к граням (110) и (100) и (011) и (001) дают возможность очень просто вычислить осевое отношение. Поскольку отношение а: b: с может быть выражено как а: 1: с, его можно записать также в виде а/b и с/b, тем самым придав вычислению большую наглядность. В ромбическом кристалле, например в топазе, измерению подлежат следующие углы. Принимая во внимание только кристаллографические оси и линию их пересечения со следом граней (НО) и (011), мы получаем треугольники с углами ф и р (рис. 9). Отношение а/b задается тангенсом ф, а отношение с/b — тангенсом р (рис. 10).

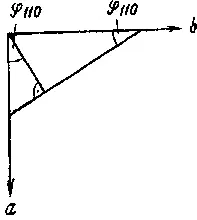
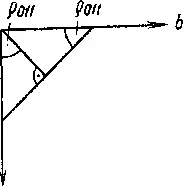
Рис. 10.

Требуется, следовательно, измерить прикладным гониометром только углы между нормалями к соответствующим граням и взять из таблиц логарифмов значения тангенсов этих углов. В результате получаем геометрическое осевое отношение, которое после установления углов переписывается следующим образом:

a: l: c=tgф (110): I: tgp (01i).

У ромбического топаза были измерены угол между нормалями к (ПО) и (100), равный ф 110 = 27,9°, и угол между нормалями к (011) и (001), равный poii = 43,7 0. Из этих данных через tg27,9°: I: tg43,7° получаем геометрические осевые отношения 0,529: 1: 0,955,

Если на кристалле отсутствуют грани (100) или (001), то углы ф и р можно получить также делением пополам углов между двумя гранями (ПО) и (011) (рис. 11).

В основе вычислений лежит предположение, что кристалл имеет грани, пересекающие две оси а и b или с и b, поскольку ось b принята за единицу. Углы между нормалями к граням (100), (010) и (001) не дают осевого отношения. Они указывают на сингонию и составляют 90° в ромбической, тетрагональной и кубической сингониях, 60° в одной плоскости гексагональной синго–нии. В триклинной сингонии во всех плоскостях и в моноклинной в одной плоскости эти углы между нормалями отличаются от 90 и 60° и являются характеристическими для каждого минерала. Они связаны с углами между осями. Вычислять их здесь не представляется возможным. Точно так же расчет осевого отношения из углов между нормалями к граням (111) или произвольными гранями (hkl] приходится оставить на долю учебников кристаллографии.

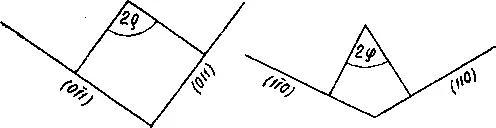
Рис. 11.

Иногда на кристаллах грани (НО) и (011) отсутствуют, но появляются грани (120) или (210) либо (012) или (021), которые в ряде случаев встречаются и наряду с гранями (110) и (011), так что выбор граней для измерения затрудняется и правильность индицирования может быть установлена только расчетным путем. Согласно закону рациональности отношений параметров, осевое отношение, вычисленное по данным ложного индицирования, должно допускать преобразование в правильное путем умножения или деления на малые целые числа. Поэтому мы записываем в более общей форме:

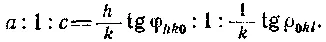
Для случая вычисления отношения, исходя из граней (210) и (021) и соответствующих им углов между нормалями, это означает

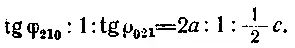
У топаза были измерены угол между нормалями к (100) и (210), равный ф 210= 14,8°, и угол между нормалями к (001) и (021), равный p 021=62,3°. Из этих данных через tg 14,8°: 1: tg 62,3° получаем геометрические осевые отношения 0,264: 1: 1,905.

Легко увидеть, что, удвоив значение а и взяв половину значения с, мы получим искомое осевое отношение.

Поскольку на гранях кристаллов, конечно, не написаны их индексы, правильное индицирование не всегда будет легко удаваться любителям, а в некоторых случа–лх, вероятно, вообще окажется невозможным. Поэтому, если полученное осевое отношение легко сопоставляется с приведенным в данном определителе путем умножения или деления на малые целый числа, вы можете быть верейными в правильности определений. Если на об–ломках кристаллов можно измерить лишь немногие углы и нельзя определить осевое отношение полностью, то же знание только a /b или с/b дает ценные диагностические указания.

Вывод вычислительных формул базируется на использовании прямоугольных треугольников, поэтому он действителен, строго говоря, лишь для прямоугольных сингоний. С некоторыми ограничениями по точности область применения формул может быть расширена. Хороший прикладной гониометр работает с точностью ± 1°. Вычисление осевого отношения, полученного с помощью этого измерительного прибора, с точностью большей, нежели до одного знака после запятой, имеет мало смысла. В пределах такой точности по приведенным формулам можно вычислять осевые отношения и большинства триклинных или моноклинных минералов. Большие неточности возникают в тех случаях, когда углы между осями резко отклоняются от 90°. Для тетрагональных минералов а — b, поэтому а: 1: с=1: 1: с, и формула упрощается до c/a=tgp 011= tgp 101. Вычисление применительно к гексагональной сингоний в рамках этой книги не может быть приведено. В подобных случаях следует ограничиться измерением характеристических углов 60° как отправной точки для выбора сингоний.