Скотт Бембенек - Механизм Вселенной: как законы науки управляют миром и как мы об этом узнали

Аналогично Карно предположил, что подобные явления справедливы и для тепловых двигателей. Более того, он считал, что невозможно извлечь работу из тепла при отсутствии разницы температур: должен быть нагреватель (источник) и холодильник (теплоприемник), чтобы двигатель работал — так же как должна быть разница высот для того, чтобы вода текла и двигала водяное колесо.

Он также был убежден, что при этом тепло обязано сбрасываться. Карно считал, что как в водяном колесе вода падает из высокой точки в низкую, так и тепло в тепловом двигателе «падает» из области высокой температуры в область низкой, в конце концов полностью «перетекая» в холодный резервуар.

При работе водяного двигателя вода перетекает сверху вниз, полностью сохраняя свой объем (кроме той части, которая испаряется). Карно как сторонник теплородной теории придерживался этой аналогии с водяным двигателем и был уверен, что так же сохраняется и тепло в тепловом двигателе и в процессе его работы все тепло из горячего резервуара перейдет в холодный.

Примерно через 30 лет после открытия первого начала термодинамики стало ясно, что сохраняется вовсе не тепло, а скорее энергия в целом. Так что количество тепла, изначально покинувшего горячий резервуар, равняется сумме количества тепла, поступившего в холодный резервуар, и работы, проделанной тепловым двигателем.

Математическая модель обратимого теплового двигателя Карно позволила ему прийти к важнейшим выводам. Чтобы понять важность его модели, проведем мысленный эксперимент. Представим, что у нас есть два обратимых тепловых двигателя Карно (см. рис. 5.2). Назовем их «двигатель 1» и «двигатель 2» и подключим к одним и тем же горячему и холодному резервуарам. Теперь представим, что каждый из них выполняет разное количество работы. Для ясности назовем эти количества W 1и W 2, при этом W 1больше, чем W 2. Другими словами, производительность двигателя 1 выше, чем производительность двигателя 2.

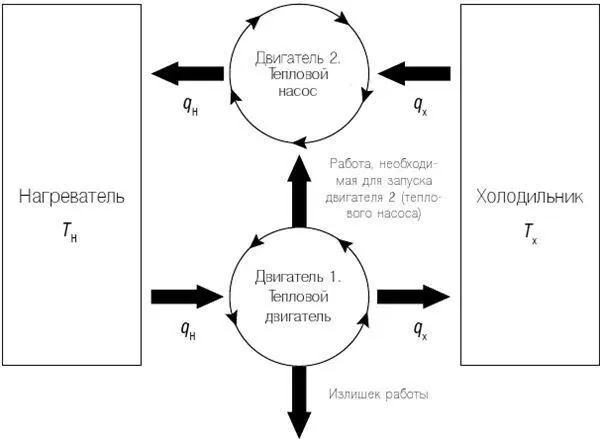
Рис. 5.2. Представим, что двигатель 1 получает начальное количество теплоты ( q н) от нагревателя. Некоторое количество этой энергии ( q х) поступает в холодильник, в то время как оставшаяся энергия используется для работы (двигатель обратимый, поэтому нет потери тепла в результате механического или термического трения). Некоторая часть этой работы используется для запуска двигателя 2, так как тепловой насос забирает обратно из холодного резервуара такое же количество теплоты ( q х, которое перешло из двигателя 1), добавляя часть собственного тепла, и теперь способен передать полное изначальное количество теплоты ( q н, переданное двигателем 1) обратно в горячий резервуар. Далее представим, что двигатель 1 может сделать все это, и у него останется излишек работы.

Ключевая особенность здесь — обратимость тепловых двигателей, которая заключается в отсутствии необходимости преодоления механического или термического трения. Поэтому требуется крохотный объем работы — в дополнение к производимой, — чтобы превратить двигатель в тепловой насос , который берет энергию из холодного резервуара и направляет ее в горячий. Это происходит аналогично нашему примеру с обратимыми качелями, где мы в любой момент движения могли изменить его направление путем приложения малой силы. Мы знакомы с тепловым насосом — холодильник, который поддерживает низкую температуру, выводя внутреннее тепло в окружающую среду [44]. В самом деле, тепловой насос похож на водный насос , по сути являющийся водяным двигателем, который может быть обратимым, что позволяет перемещать воду с меньшей высоты на бо2льшую.

Поскольку у двигателя 1 больше объем производимой работы ( W 1), мы используем его для работы двигателя 2 в обратном режиме, превращая его в тепловой насос. Теперь мы можем создать следующий цикл: двигатель 1 забирает начальный объем тепла ( q н) из нагревателя, передает его часть q хв холодильник и выполняет работу. Эта работа заставляет двигатель 2 забрать такой же объем тепла ( q х, который передал двигатель 1) обратно из холодильника и добавить часть собственного тепла, таким образом передав полный объем тепла ( q н) обратно в нагреватель. Более того, мы можем представить, что двигатель 1 может проделать все это, и у него останется излишек работы. Наконец, весь этот процесс обратим благодаря тому, что не происходит потерь тепла из-за механического или термического трения.

Если что-то здесь кажется вам неправильным, вы не одиноки; Карно считал так же. Короче говоря, конечный результат этого цикла заключается в том, что двигатель 1 способен производить работу, не затрачивая на это энергию. Это происходит за счет того, что двигатель 2 (тепловой насос) возвращает энергию, которую он забрал из нагревателя ( q н). И даже после того, как он проделывает все это, у него остается излишек работы. Более того, поскольку нагреватель никогда не иссякает, цикл является бесконечным! Немного отличаясь в деталях, это похоже на вечный двигатель первого рода (о котором мы писали ранее), где мы представляли, что машина может двигаться бесконечно на одном баке топлива [45].

Придерживаясь принципов своей основной теории, Карно пришел к выводу, что производительность (эффективность) любых двух тепловых двигателей, работающих на одинаковых температурах, должна быть одинаковой, что делает невозможным существование нашего вечного двигателя. Точнее об этом говорит теорема Карно . Согласно ей, производительность (а значит, и эффективность) любого обратимого (идеального) теплового двигателя зависит только от температур нагревателя и холодильника. Хотя я не стал бы выводить эту формулу здесь [46], математически мы можем записать это утверждение так:

Производительность = 1 — T х / T н,

где T хи T н— температуры холодильника и нагревателя соответственно, а 1 означает 100 %-ную производительность. По этой причине количество тепла, которое может произвести тепловой двигатель, и объем работы, который он может выполнить, определяются исключительно разницей температур. Настоящий тепловой двигатель не мог бы быть таким же эффективным по объему произведенных работ и тепла из-за своего устройства, о чем мы чуть позже поговорим. Другими словами, обратимый тепловой двигатель демонстрирует максимальный объем работы и производительности, достижимый за счет разницы температур [47].

В самом деле, система, работающая обратимо, — идеальна. Работа, производимая обратимым тепловым двигателем, и ее? эффективность являются эталоном, которого не может достичь ни один тепловой двигатель. Тем не менее, исходя из нашего уравнения, даже идеальный обратимый тепловой двигатель не может достичь 100 %-ной эффективности [48]. Это обусловлено тем, что разница температур (между T хи T н) все еще требует необходимого потока тепла [49]. Это позволяет по-новому рассмотреть утверждение о том, что необходима передача тепла в холодный резервуар, и, следовательно, не все переданное тепло используется в работе (как мы говорили ранее).