Скотт Бембенек - Механизм Вселенной: как законы науки управляют миром и как мы об этом узнали

Когда фотон отскакивает от электрона, то при столкновении они обмениваются импульсом. Импульс, потерянный фотоном, будет по модулю равен приобретенному электроном — суммарный импульс сохраняется. Ясно, что если мы можем определить, насколько изменился импульс фотона, тогда мы сможем определить импульс электрона до столкновения [212], что даст нам и положение, и импульс электрона одновременно. Однако есть небольшая проблема. На самом деле мы не знаем направление полета падающего фотона после того, как он отскочит от электрона. Мы точно знаем только то, что он принадлежал «диапазону направлений», при движении в каждом из которых он в результате пройдет через линзу, тем самым позволяя нам определить положение электрона (в пределах неопределенности, отмеченной выше). А теперь этот диапазон направлений можно сузить, чтобы уменьшить неопределенность направления импульса фотона. Все, что нам нужно сделать, — это уменьшить диаметр линзы микроскопа.

Ой, ну подождите, ведь неопределенность в положении электрона обратно пропорциональна диаметру линзы, и уменьшение ее диаметра приведет к большей неопределенности в положении. Для решения этой проблемы мы могли бы использовать фотон с меньшей длиной волны. К сожалению, оказывается, что это увеличит неопределенность импульса, благодаря — вы угадали — квантовой природе импульса фотона. Гейзенберг смог использовать свой подход матричной механики, чтобы показать, что определенную пару величин, характеризующих свойства (например, координата и составляющая импульса, направленная вдоль той же оси, от которой данная координата отсчитывается), нельзя определить с произвольной точностью. А именно он обнаружил, что произведение их неопределенностей не может быть меньше, чем постоянная Планка [213]. Это означает, что если мы получаем более точные знания об одной из характеристик, то в результате наше знание о соответствующей дополняющей характеристике становится меньше. Итак, мы знаем одну характеристику почти абсолютно точно — и поэтому о другой не знаем совсем ничего; или, в качестве компромисса, знаем немного — об обоих.

Это не имеет никакого отношения к нашим возможностям (или их отсутствию) измерения этих величин. Наоборот (вернемся к нашему примеру с микроскопом), это означает, что квантовые частицы наподобие электрона просто не обладают точным положением и точным импульсом в один и тот же момент времени; для них эти характеристики существуют только расплывчато , неопределенно. Давайте осознаем, что если Борн использовал квантовую вероятность, чтобы устранить из квантовой механики детерминизм, то в принципе неопределенности Гейзенберга это происходит безо всякого обращения к понятиям, связанным с вероятностью. Поэтому они выступают как два независимых удара против причинности. Возможно самым лучшим примером, иллюстрирующим квантовую вероятность и корпускулярно-волновой дуализм, является опыт с двумя щелями .

Представим «электронную пушку», стреляющую электронами в направлении экрана с двумя отверстиями (или щелями), которые находятся от нее на одинаковом расстоянии D , а также на одинаковом расстоянии D ′ от центра экрана (см. рис. 16.1). Электронная пушка установлена на башне, которая движется вперед и назад, а также из стороны в сторону, что очень похоже на движение вращающегося вентилятора. С учетом такого движения ясно, что мы не ставим перед собой цель попасть электронами в щели; вместо этого мы просто стреляем очень много раз случайным образом. Сами щели имеют одинаковые размеры, достаточно большие, чтобы через них мог пройти электрон.

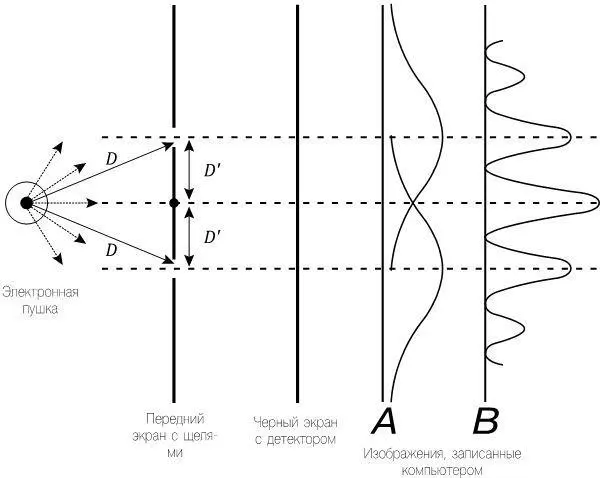
Рис. 16.1. «Электронная пушка» стреляет наобум по экрану с двумя щелями, находящимися на одинаковом расстоянии D от нее, а также на одинаковом расстоянии D ′ от центра экрана. У заднего экрана электроны тормозят, и детектор регистрирует их положение и отправляет информацию на компьютер. Изображение A показывает распределение, которое мы получаем, когда располагаем детектор у каждой из щелей, чтобы зафиксировать прохождение электрона. В этом случае мы не видим интерференционной картины и фактически получаем результат, который мы бы ожидали, если бы электрон вел себя исключительно как частица, — здесь он просто проходит либо через одну щель, либо через другую. Однако, когда детекторы отсутствуют, мы получаем изображение B . Здесь при прохождении электронов через щели мы реально видим интерференционную картину.

Подлетая к щели, некоторые электроны проходят через нее, а другие — нет. Прошедшие электроны продолжают свой путь, пока в конце концов не столкнутся с другим экраном, расположенным гораздо дальше [214]и играющим роль заслонки. Детектор на этом заднем экране фиксирует окончательное положение каждого электрона, а потом отсылает информацию о нем на компьютер для дальнейшей обработки.

По мере того, как мы выстреливаем все больше и больше электронов (мы хотим собрать хорошую статистику), все больше и больше электронов проходят через щели и ударяют по заднему экрану. Накопив сведения о многочисленных положениях электронов, компьютер способен создать картину, или распределение. Если наша статистика достаточно хороша, то из этого распределения мы узнаем вероятность нахождения электрона в определенном положении на заднем экране, когда он случайным образом выстреливается по двум щелям. Итак, как выглядит это распределение?

Перед тем, как мы дойдем до этого, давайте воспользуемся моментом, чтобы попробовать предсказать результаты. Ясно, что если электрон ведет себя исключительно как частица, разумно ожидать, что он проходит либо через одну щель, либо через другую. Более того, электрон, проходящий через щель, либо «убьется» об боковую часть или об край, либо пройдет вперед полностью невредимым. Если он проходит вперед, мы обнаружим его прямо за щелью — образно говоря, в «центральном положении», — когда он ударяет по заднему экрану; тогда как если он врезается, то мы обнаружим, что он ударяет по экрану на некотором расстоянии от центрального положения, с одной из сторон от него. С учетом всего этого мы ожидаем, что распределение для данной щели будет таким, что максимальное число ударов происходит прямо в центральное положение, тогда как с удалением от него число ударов постоянно уменьшается. И последнее, распределение по обоим сторонам от центрального положения будет выглядеть одинаково. То есть оно будет симметричным .

Хорошо, у нас появилась довольно четкая картина того, что мы увидим. Но при проведении опыта мы обнаруживаем, что получающееся в результате распределение на экране компьютера совсем не похоже на то, что мы представляли. Вместо этого мы обнаруживаем, что максимум распределения приходится на пространство между двумя щелями — даже не на центральное положение для какой-либо из двух щелей! Распределение по-прежнему симметрично относительно максимума (как минимум, это есть), но при движении от центра мы не видим, чтобы число ударов постоянно уменьшалось, как мы представляли. Вместо этого на каждой стороне заметны пики с большим числом ударов, ну а вне этих пиков видно, что число ударов стабильно уменьшается до самого нуля, где не показывается ни одного электрона. Что же произошло?