Роберт Сойер - Вселенная. Емкие ответы на непостижимые вопросы

Рис. 2. Предел круга I.

В данной геометрии (так называемой «конформной картине Бельтрами»), как это проиллюстрировано Эшером, все белые рыбы считают себя идентичными друг другу, и то же с черными рыбами, хотя рыбы, изображенные ближе к краям, намного меньше тех, что в центре. У всех рыб круглые глаза, и эта округлость сохраняется вплоть до краев, как свойство этой конформной геометрии. Граничный круг представляет собой бесконечность для всех рыб этого геометрического мира.

Такое «сдавливание» к бесконечности для получения конечной границы – один из аспектов конформной геометрии. И теперь я сделаю то же самое для вселенной. Мы будем рассматривать пространственно-временную геометрию вселенной тем же конформным образом, используя тот же трюк, что Эшер. Это показано в верхней части рисунка 3. У нас есть три измерения пространства и одно измерение времени (хотя, как и прежде, вы видите только одно измерение пространства на картинке, а остальное воображаете). Этот трюк позволяет нам сдавить удаленную временну́ю бесконечность всего экспоненциального расширения вниз, конформно, к конечной границе, как показано в верхней части рисунка 3.

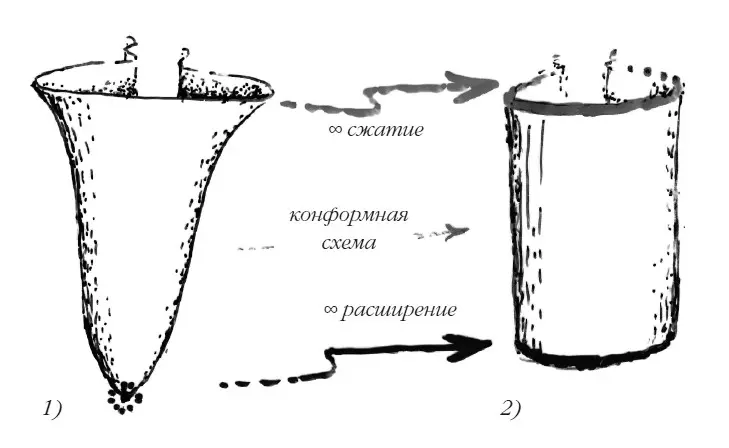
Рис. 3. Два математических трюка: 1) «сдавить» будущую бесконечность, чтобы получить границу в будущем; 2) «растянуть» сингулярность Большого взрыва, чтобы получить начальную границу.

Теперь я сделаю противоположную вещь с другим концом нашей картины вселенной. То есть, я раздвину Большой взрыв и тоже сделаю его областью с конечной границей. Это показано в нижней части рисунка 6.

Одна из причин, по которым я хочу сделать так – и здесь я не собираюсь вдаваться в подробности, – состоит в том, что я хочу включить одну из самых важных вещей в физике, которая перевешивает любую конкретную динамическую теорию, которую вы рассматриваете. Это Второй закон термодинамики. Этот закон (Второй закон для краткости), грубо говоря, гласит, что с течением времени вещи становятся все более хаотичными. Используя более технический язык, мы скажем, что энтропия увеличивается со временем, где слово «энтропия» – несколько более точный физический термин, для того, что я называл хаосом. Так что Второй закон утверждает, что энтропия увеличивается со временем (или по крайне мере сохраняется) за исключением возможных случайных флуктуаций.

Второй закон можно выразить и по-другому, сказав, что энтропии становится меньше и меньше по мере продвижения в прошлое. Таким образом, чем ближе мы подходим к Большому взрыву, тем меньше должна быть общая энтропия. Однако здесь появляется некий парадокс, по причине имевшего место в отдаленном прошлом чрезвычайно горячего состояния вселенной, которое мы определяем как Большой взрыв, чудовищно горячего состояния, выглядящего как тепловое, где слово «тепловой» обычно определяет максимальную энтропию! В самом деле, свидетельства, которые мы получаем, измеряя так называемый Космический микроволновый фон или CMB (электромагнитное излучение, приходящее к нам из космоса со всех направлений), по всей видимости, подтверждают это. Два наиболее явных и поразительных факта о CMB состоят, во-первых, в однородности во всех направлениях, которую он выявляет в структуре очень ранней вселенной, и во-вторых, в тепловой природе ее спектра (планковский спектр излучения). Оба они характерны для состояния максимальной энтропии! Это выглядит как выраженный парадокс, который мы обнаруживаем в этой очень ранней вселенной, состояние максимальной энтропии в этих двух аспектах, а именно однородности и планковском спектре. Не чрезвычайный ли это парадокс? Мы ведь должны были обнаружить состояние с очень небольшой энтропией, чтобы Второй закон оказывался верен и для самого начала существования вселенной.

Этот очевидный парадокс разрешается тем соображением, что наши предыдущие рассуждения включали только вещество и излучение в ранней вселенной, а роль гравитации не упоминалась. В отличие от случая вещества и излучения, где однородность означает высокую энтропию, в случае гравитации все наоборот. Если вы рассматриваете гравитацию, ситуации с низкой энтропией – то есть «высокоорганизованные» ситуации – это те, в которых геометрия очень, очень однородна.

По мере того как это однородно распределенное вещество начинает слипаться под воздействием гравитации, энтропия в гравитационном поле увеличивается. Слипшиеся области разогреваются и становятся звездами, а однородные области остаются холодными. Это проявление Второго закона термодинамики: резервуар с низкой (благодаря изначальной однородности) энтропией в гравитации в ходе гравитационного слипания переносится к объектам из концентрированного вещества, таким как звезды, вместе с более холодным межзвездным газом, где мы теперь видим дисбаланс температуры и плотности, который указывает на низкую энтропию в веществе. И от этого дисбаланса температуры зависит жизнь на Земле. Мы получаем энергию от Солнца в форме с низкой энтропией (относительно немного фотонов высокой энергии, где фотоны – квантованные элементы света), а ночью энергия возвращается в темное небо в форме с высокой энтропией (много-много фотонов низкой энергии). Таким образом растения с помощью фотосинтеза наращивают свою массу организованным низкоэнтропийным способом и поддерживают жизнь на этой планете. Все это происходит благодаря низкой энтропии в гравитационном поле, которое выражается в очень однородном начальном состоянии.

Одним из первых аргументов, выдвинутых в поддержку необходимости космической инфляции, было то, что раннее разглаженное состояние вселенной может быть объяснено, только если на очень ранней стадии ее существования произошло экспоненциальное расширение, которое разгладило бы любую неровность, которая могла бы возникнуть в самом начале. Этот аргумент и сейчас обычно приводят как причину для постулирования очень ранней инфляционной фазы. Однако именно этот аргумент в пользу космической инфляции, очевидно, неверен, поскольку требует от нее конфликтовать со Вторым законом термодинамики, волшебным образом уменьшая вклад гравитации в энтропию в ходе инфляционного расширения.

Этот контраргумент можно сделать более выразительным, если рассмотреть коллапсирующую модель вселенной – как нашу на рисунке 1, но с обратным направлением времени. С появлением небольших возмущений, развивающихся согласно Второму закону, этот коллапс ведет к огромной конгломерации сингулярных черных дыр, формирующихся на его финальных стадиях, и завершается невероятно сложной пространственно-временной сингулярностью, как показано на рисунке 4.