Андрей Варламов - Физика повседневности. От мыльных пузырей до квантовых технологий

Бенджамин Франклин играет на своей стеклянной гармонике

Феноменом поющих бокалов интересовался великий американский ученый и выдающийся государственный деятель (достоинства, которые в наши дни редко встречаются в одном человеке) – Бенджамин Франклин (1706–1790), более известный своими экспериментами по изучению атмосферного электричества и изобретением громоотвода. Он применил свойство бокалов «петь» в придуманном им музыкальном инструменте – стеклянной гармонике. Она состояла из батареи стеклянных чаш, нанизанных через отверстие в центре на ось, на равном расстоянии друг от друга. Устройство было оснащено педалью, приводившей к вращению устройства, как, например, в старинных швейных машинках или гончарных кругах. Касаясь влажными пальцами вращающихся полусфер, музыкант получал кристально чистый звук, от самого высокого на маленьких чашах до самого низкого на чашах большего диаметра.

В 1763 году Франклин подарил стеклянную гармонику англичанке миссис Дэвис, которая много лет демонстрировала ее на гастролях по всему миру. Затем инструмент бесследно исчез; вероятно, его постигла та же участь, что и многие бокалы, разбившиеся из-за неосторожного движения… Другие экземпляры инструмента еще долго оставались в обращении. Его музыкальные качества оценивались по-разному и, конечно, зависели от мастерства исполнителя. Чарующие звуки стеклянной гармоники даже подверглись обвинению в том, что они провоцируют преждевременные роды или вызывают безумие играющих на ней музыкантов! Тем не менее музыку для гармоники писали известные композиторы и ее высоко ценили некоторые именитые слушатели, такие как великий скрипач Никколо Паганини. Но постепенно мода прошла, и к 1830 году этот инструмент полностью исчез из салонов. В течение нескольких последних десятилетий стеклянную гармонику снова изготавливают; вращение полусфер теперь обеспечивает электрический двигатель, а для увлажнения пальцев исполнителя служит пульверизатор. Читатель может составить собственное представление о качествах этого инструмента с помощью интернета: найдите интерпретацию французского виртуоза Томаса Блоха рондо K. 617 Моцарта для стеклянной гармоники.

Человеческое ухо воспринимает звуки частотой примерно от 20 до 20 000 Гц. «Хрустальный» звон стекла обусловлен присутствием в нем звуковых волн, принадлежащих к верхней части этого диапазона, то есть с частотами в интервале от 10 до 20 кГц. При звоне пустых или наполненных негазированным напитком бокалов после удара стеклянных стенок колебания продолжаются достаточно долго. И наоборот, звук затухает очень быстро, когда в бокалах находится шампанское… Объяснение этого различия кроется в содержащихся в игристом вине пузырьках углекислого газа CO 2 (см. главу 14, «Пузырьки шампанского»). Действительно, после соударения бокалов в их содержимом распространяются звуковые волны: зоны сжатия жидкости чередуются с зонами разрежения (см. главу 2, «Когда звук распространяется зигзагами»). Но растворимость газов в жидкости зависит от давления: она тем сильнее, чем давление выше (закон Генри – Дальтона). Итак, понижение давления приводит к «дегазации» шампанского: в бокале возникают пузырьки, которые рассеивают энергию колебаний. Поэтому звук в игристом вине затухает намного быстрее, чем в вине «спокойном», где пузырьки отсутствуют (илл. 3).

В положении равновесия форма воздушного пузырька небольшого размера в воде является сферической. Его радиус таков, что давление воздуха внутри пузырька компенсирует давление воды. В результате внешнего воздействия (например, звуковой волны) пузырь деформируется и затем начинает колебаться около своего равновесного положения.

Эти колебания могут быть представлены в виде суммы большого числа различных деформационных мод. Некоторые из них приводят к значительным смещениям поверхности пузыря; такие моды называют резонансными. Один из таких резонансов, резонанс Миннарта, происходит на весьма низкой частоте: при этом он соответствует возбуждению звуковых волн весьма больших длин (как в воздухе, так и в воде) по сравнению с размерами самого колеблющегося пузырька. Эти колебания оказываются аналогичными колебаниям подвешенного на пружине и выведенного из положения равновесия шара (см. илл. ниже): при отсутствии затухания шар начинает колебаться с определенной частотой ƒ, которая зависит только от величины его массы и жесткости k пружины. Чтобы понять аналогию с пузырьком, заметим, что масса шара M в случае пузырька соответствует массе вовлеченной в движение жидкости, в то время как роль возвращающей силы упругости пружины в случае пузырька играет сила избыточного давления, стремящаяся вернуть его поверхность в положение равновесия. В случае пружины эта сила пропорциональна удлинению x пружины: F = – kx , где постоянная k является характеристикой пружины. Частота колебаний шара равна

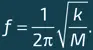
Она тем выше, чем жестче пружина и меньше масса.

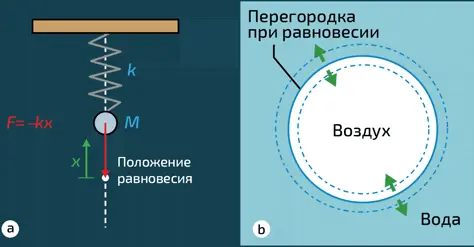
Колебания подвешенного на пружине шара (a) аналогичны колебаниям пузырька (b), который осциллирует между двумя крайними позициями (пунктирные окружности) около своего равновесного положения (сплошная линия)

А какой же будет формула для колебаний пузырька? Воспользуемся методом размерности и подберем для пузырька характерные физические параметры, которые заменят M и k . Таким образом мы немного сократим сложный расчет (который, однако, остается необходимым для получения точного количественного результата). Характерные величины, которые, очевидно, должны войти в ответ, – это плотность ρ жидкости, радиус пузырька R в положении равновесия и начальное давление жидкости P . Действительно, возвращающая сила, воздействующая на поверхность пузыря, возникает из-за давления внутри него, которое в равновесном положении должно быть равным давлению жидкости. Масса же вовлеченной в движение жидкости по порядку величины соответствует произведению объема пузырька на ее плотность: (4/3)π R 3ρ. Что же касается коэффициента жесткости k , то он должен представлять собой отношение возвращающей силы к длине. Единственная величина, имеющая размерность длины в нашей задаче, – это радиус R , а величина с размерностью силы – это произведение давления P на площадь поверхности пузыря, то есть PR 2. Таким образом, коэффициент жесткости k должен быть порядка PR . Подставив эти значения в предыдущую формулу, получим результат, близкий к выражению, которое вывел Марсел Миннарт: