Андрей Варламов - Физика повседневности. От мыльных пузырей до квантовых технологий

F лс = (Re/12) F С.

Для сферы диаметром 1 мм в воде число Re составляет порядка 200. Поэтому для оценки силы сопротивления мы используем формулу для силы лобового сопротивления, которая дает в достаточной мере точный результат.

Таким образом, действующая на пузырек результирующая сила F = F А + F лс . Второй закон Ньютона (см. главу 4, «Ньютоновская механика») позволяет получить уравнение движения объекта при условии, что известна его масса m : векторная сумма внешних сил, воздействующих на объект, равна его ускорению, умноженному на массу, то есть

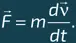
В рассматриваемом случае, когда движущимся в жидкости объектом является пузырек пренебрежимо малой массы, найденная результирующая сила главным образом придает ускорение жидкости, вовлекаемой в движение на пути пузырька вверх. Как же написать для нее второй закон Ньютона? Какую массу и ускорение чего в него подставлять? Задача представляется неразрешимой! К счастью, из механики жидкостей известно, что второй закон Ньютона применим и к погруженному в жидкость сферическому объекту при условии добавления к его собственной массе некоторой дополнительной, так называемой присоединенной массы δ m = (2/3) πρ R 3. Эта величина учитывает необходимость вовлечения в движение окружающих сферический объект слоев жидкости и, как это ни странно, оказывается равной половине массы жидкости, которая потребовалась бы, чтобы эту сферу заполнить. Для движущегося в воде пузырька полная масса m практически равна присоединенной массе δ m . В первые мгновения после отрыва пузырька ото дна его скорость еще мала, сопротивление воды незначительно и второй закон Ньютона приобретает вид: F А = δ m d v/ d t, что после подстановки выражений для силы Архимеда и присоединенной массы приводит к удивительному результату: dv/dt = 2 g . Следовательно, ускорение пузырька на начальном этапе его движения в два раза превышает ускорение свободного падения и направлено, конечно же, вверх, а не вниз.

После нескольких сантиметров подъема, когда силы F А и F с , воздействующие на пузырек, уравновешиваются, он достигает скорости v , которая определяется только его радиусом R . Для пузырька диаметром 1 мм экспериментально найденное значение скорости составляет 20 см/с, что отвечает приведенной выше формуле.

Почему же, когда скорость пузырька достаточно велика, формула Стокса для силы сопротивления перестает быть верной? Оказывается, что она применима только в так называемом ламинарном режиме движения, когда линии потока плавно огибают движущееся тело (см. илл.). При достаточно больших скоростях позади тела, в его следе, появляются неупорядоченные вихри – такое движение жидкости называется турбулентным . Возникновение вихрей требует расхода энергии и замедляет движение пузырька.

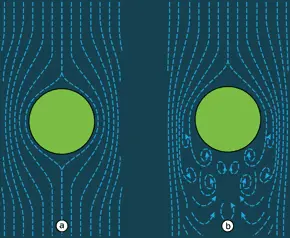
a. Ламинарное обтекание препятствия.

b. Возникновение турбулентных вихрей позади этого препятствия. Синими линиями показано направление течения

Значение давления насыщенных паров воды при различных температурах

Зарождающиеся пузырьки не сразу отрываются ото дна: пока их объем невелик, их удерживают силы поверхностного натяжения. Чтобы оторваться и принять сферическую форму, он должен совершить работу по преодолению этих сил, тем самым увеличив свою поверхностную энергию (см. главу 6). Эта работа совершается благодаря понижению потенциальной энергии в поле тяжести Земли окружающей пузырек жидкости. Приравнивая для оценки поверхностную энергию пузырька к изменению потенциальной энергии жидкости, находим:

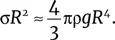
Отсюда можно найти критический размер, при котором пузырек покидает дно:

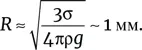
Можно оценить и время отрыва пузырька ото дна: расстояние порядка своего радиуса R он проходит с ускорением порядка g . Таким образом, для миллиметрового пузырька затраченное время составляет порядка ( R / g ) 1/2, или 0,01 секунды.

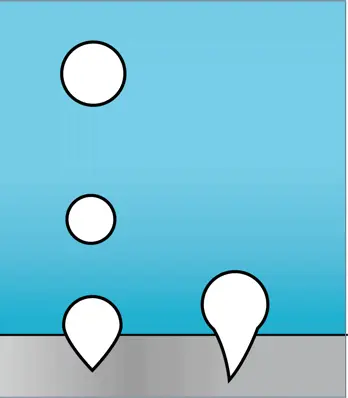
2. Как только температура воды становится достаточно высока, на дефектах дна чайника возникают пузырьки. Благодаря действию сил поверхностного натяжения, пока их объем невелик, пузырьки остаются у дна и, заполняясь паром, постепенно растут

Давайте проследуем за пузырьком во время его восхождения. Поднимаясь, он попадает в более холодные слои воды. В самом деле, температура в чайнике распределена вовсе не однородно. Вода не очень хороший проводник тепла. Торопясь выпить чаю, мы подвергаем чайник интенсивному нагреванию, и, когда температура дна чайника уже превышает 100 °C, верхние слои воды еще остаются сравнительно холодными. Поэтому, по мере того как пузырек поднимается, пар внутри него охлаждается и частично конденсируется обратно в воду. Но главное – падает давление остающегося в пузырьке насыщенного пара, и он, не в состоянии противостоять давлению жидкости и Лапласа, схлопывается (см. врезку). Если же он содержал заметное количество воздуха, то по крайней мере сильно сжимается. И лишь когда начинается кипение, то есть образование пузырьков во всем объеме воды, их радиус начинает с набором высоты возрастать (см. главу 15, «Вода при кипении чайника перегревается»).

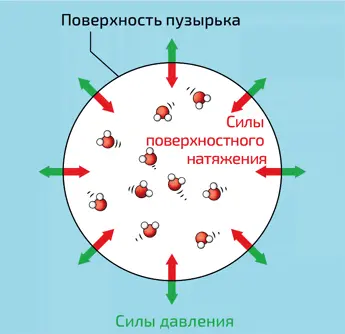
3. Пузырек водяного пара – до начала кипения. Молекулы водяного пара внутри него находятся в беспорядочном тепловом движении и, ударяясь о поверхность, обеспечивают давление. Именно оно и уравновешивает суммарное давление Лапласа, атмосферы и водяного столба (красные стрелки). Поднимаясь вверх, пузырек достигает более холодных областей, где водяной пар охлаждается, частично конденсируется и пузырек схлопывается

Как говорилось ранее, возникновение пузырьков сопровождается характерным шумом. Какое физическое явление лежит в его основе? Представляется сомнительным, что само по себе всплывание пузырька в жидкости приводит к возникновению звуковой волны; так, например, в воздухе звуковые волны от движущегося тела слышны только при достижении скорости пули (например, летящий теннисный мяч не издает звук). С другой стороны, два описанных выше явления – отрыв пузырьков ото дна, а затем их схлопывание – кажутся хорошими кандидатами: они действительно возбуждают колебания внутри жидкости. А какова их частота? Простые вычисления показывают, что пузырек радиуса 1 мм отделяется в течение примерно 0,01 с, что соответствует частоте колебаний около 100 Гц. Затем он схлопывается приблизительно за 1 мс, что соответствует частотам порядка 1000 Гц, то есть более высокому звуку. Эта оценка подтверждается простым наблюдением: незадолго до начала кипения, когда пузырьки перестают схлопываться, внимательное ухо услышит, что испускаемый звук, больше не связанный с отрывом пузырьков ото дна, становится более низким.