Андрей Варламов - Физика повседневности. От мыльных пузырей до квантовых технологий

Таким образом, сверхпроводимость – это редкий случай проявления законов квантовой механики в окружающем нас макроскопическом мире.

В предыдущей главе мы в общих чертах рассказали о явлении сверхпроводимости как таковом и о долгом пути ученых к пониманию его квантовой природы. В этой главе мы продолжим наш рассказ о необычных свойствах сверхпроводников и остановимся на способах их применения, которые мало знакомы широкой публике.

Как мы уже видели, Нильсу Бору удалось объяснить многие свойства атома, предположив, что скорость v электрона на круговой орбите радиуса R удовлетворяет отношению m ν R = nħ , где n – целое число, m – масса электрона и ħ – постоянная Планка (см. главу 22). Замечательно, что это правило может быть обобщено для описания движения любой частицы, совершающей круговое движение в определенном квантовом состоянии. Отметим, что как раз к движению электрона в атоме постулат Бора применим не очень хорошо, поскольку электрон четко определенную орбиту не описывает (иначе нарушались бы соотношения неопределенности (см. главу 22, «Спектр излучения атомов – ключ к атомной структуре»)). С другой стороны, как показал Фриц Лондон (1900–1954) в 1948 году, он может быть успешно применен к сверхпроводящему току, текущему в круговом кольце радиуса R (илл. 1).

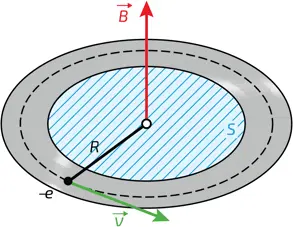
1. Ток в кольце радиуса R. Поток магнитной индукции через кольцо Φ = BS , где S – охватываемая кольцом площадь, а B – магнитное поле. Применяя к движущемуся заряду правило квантования Бора, находят, что этот поток квантуется

Правило квантования Бора, примененное к движению куперовских пар в сверхпроводящем кольце (см. главу 24, «Теория БКШ»), имеет неожиданное следствие: магнитный поток через сверхпроводящее кольцо квантуется – так же как и радиус орбиты в атоме! Точнее, магнитный поток Φ оказывается целым кратным «кванта магнитного потока»:

Φ 0 = π ħ /e = h/(2e) = 2∙10 –15Тл∙м 2,

где – е – заряд электрона (см. врезку «Квантование потока в витке сверхпроводника»).

Квант потока Φ 0 – чрезвычайно малая величина, настолько малая, что первую экспериментальную проверку гипотезы Лондона американским физикам Бэскому Диверу и Уильяму Фэйрбэнку удалось провести только 13 лет спустя, в 1961 году.

Примечательно, что в то время, как квантованные физические величины, упоминаемые нами до сих пор, принадлежали к микроскопическому миру, квант магнитного потока ученым удается измерить в относительно больших, почти макроскопических образцах (то есть видимых невооруженным глазом). Примером таких «мезоскопических», то есть промежуточных между микро- и макромирами объектов, являются вихри Абрикосова, которые могут находиться друг от друга на расстояниях в микрометры. Напомним, что эти вихри возникают в сверхпроводнике II рода, помещенном во внешнее магнитное поле (см. главу 24, «Вихри Абрикосова»). Каждый абрикосовский вихрь является носителем кванта магнитного потока Φ 0 . Еще одним подобным примером являются сверхпроводящие кольца, которые позволяют наблюдать дискретное изменение пронизывающего их магнитного потока буквально по одному кванту Φ 0 (см. ниже). Подобные наблюдения аналогичны историческому эксперименту Дивера и Фэйрбэнка 1961 года. Вместо кольца они использовали сверхпроводящий цилиндр.

Квантование потока в витке сверхпроводника

Найдем с помощью упрощенных рассуждений формулу, описывающую квантование потока в сверхпроводнике. Рассмотрим случай кругового кольца с нулевым сопротивлением, содержащего свободные заряженные частицы. С возрастанием магнитного поля растет и магнитный поток Φ, что приводит к возникновению электродвижущей силы индукции (см. главу 16, «Электромагнитная индукция»):

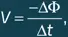
где ΔΦ – изменение потока, происходящее за время Δ t . При этом индуцируемое в кольце электрическое поле равно:

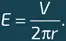
Теперь рассмотрим заряд q массы m , движущийся по кольцу со скоростью ν (илл. 1). Воздействующая на него сила равна q E , и, согласно основному принципу динамики (см. главу 4, врезку «Ньютоновская механика»), испытываемое зарядом ускорение равно q E /m. Это ускорение должно быть равно отношению увеличения скорости Δ v ко времени Δ t , следовательно:

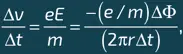
откуда находим, что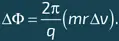

Предполагая, что правило квантования Бора mrv = nħ , упомянутое в начале этой главы, применимо к движению рассматриваемого заряда в сверхпроводящем кольце, находим, что наименьшее ненулевое значение m r Δ v равно ħ . Отсюда следует, что наименьшее ненулевое значение ΔΦ равно 2π ħ /q. Заряд куперовской пары равен 2e: таким образом, мы приходим к формуле квантования потока в сверхпроводнике, приведенной в тексте.

А что случится, если поместить кольцо в переменное магнитное поле B ? Для «нормального» проводника пронизывающий кольцо магнитный поток Φ изменяется вместе с полем. В результате возникает электродвижущая сила индукции d Φ /dt , которая порождает в кольце ток I N , такой, что RI N = d Φ/ dt , где R – сопротивление кольца. Для сверхпроводника, как мы уже знаем, поток должен оставаться неизменным, иначе его изменение вызвало бы бесконечный ток, разрушающий сверхпроводящее состояние. Поэтому по сверхпроводящему кольцу при изменении магнитного поля также будет течь ток I S , такой, чтобы пронизывающий кольцо полный поток Φ (являющийся суммой внешнего потока Φ внеш = BS и собственного индукционного потока Φ I = LI S , где L – индуктивность кольца) не изменялся.

Ситуация становится еще интереснее, если сверхпроводящее кольцо прерывается тонким слоем диэлектрика. Предположим, что мы сумели создать такую тончайшую перемычку в кольце, изготовленном из нормального металла (илл. 2). Интуитивно кажется, что ток в нем течь не сможет. И тем не менее, если толщина диэлектрической перемычки не слишком велика (например, около микрометра), ток в такой структуре может протекать! Некоторым электронам «волшебным» образом удается пройти через диэлектрик. Это чисто квантовое явление называется «туннельным эффектом». Например, при изучении объектов с помощью туннельного микроскопа ток проходит между острием устройства и поверхностью образца через зазор вакуума, имеющий размер порядка нанометра (см. главу 28, «Взгляд в наномир»). Туннелировать с некоторой вероятностью сквозь «стены» в квантовом мире могут не только электроны, но и другие, более массивные частицы, даже такие, как атомные ядра. Правда, с увеличением массы совершать эти чудеса им становится все сложнее и сложнее.