Андрей Варламов - Физика повседневности. От мыльных пузырей до квантовых технологий

Что же касается электрон-фононного взаимодействия, то соответствующие ему энергии определяются так называемой дебаевской частотой W D и не превышают 0,1 эВ. О кулоновском отталкивании электронов можно было бы предположить, что его характерная величина составляет e 2/ a , где величина a соответствует межатомному расстоянию. Легко оценить, что эта величина также оказывается порядка электронвольта. Как же тогда устроить притяжение между электронами?

Бардин, Купер и Шриффер заметили, что электроны в металле находятся в окружении ионов решетки и других электронов, поэтому отталкивание между ними сильно ослабляется и оказывается того же порядка, что и притяжение, возникающее благодаря электрон-фононному взаимодействию. Поэтому полное электрон-электронное взаимодействие для одних металлов оказывается положительным, а для других – отрицательным. Первые (например, золото, платина) ни при каких температурах не переходят в сверхпроводящее состояние, поскольку их электроны не могут образовать составные бозоны. Вторые же, где в соревновании взаимодействий побеждает электрон-фононное взаимодействие, при некоторой температуре становятся сверхпроводниками.

Чтобы ее вычислить, а также описать иные свойства сверхпроводника, можно представить себе электронные энергетические состояния в металле заполняющими воображаемый апельсин размером, соответствующим Ɛ Ф . Толщина его корки соответствует энергии, связанной с дебаевской частотой, то есть W D . Понятно, что электроны, находящиеся в глубине апельсина с энергиями значительно меньше Ɛ Ф , несмотря ни на какие электрон-фононные взаимодействия, останутся на своих энергетических уровнях. А вот электроны, находящиеся в «кожице апельсина», благодаря фрёлиховскому взаимодействию могут образовать составные бозоны. При этом оказывается, что им более выгодно объединяться парами с противоположными спинами (так называют особую характеристику элементарной частицы, которую можно интерпретировать как «врожденный» магнитный момент), так, чтобы суммарный спин такой пары, называемой «парой Купера», был равен нулю. Противоположными должны быть и векторы скоростей электронов, иначе слабое электрон-фононное взаимодействие их вместе не удержит.

Для того чтобы понять значение щели, необходимо ввести понятие плотности электронных состояний. В изолированном атоме электроны могут занимать только дискретные уровни энергии (см. главу 22, «Спектр излучения атомов – ключ к атомной структуре»). В твердом теле, состоящем из многих атомов, эти квантовые состояния образуют плотную лестницу, занимающую целую полосу (зону) на шкале энергии. Таких зон может быть несколько, последняя из них называется зоной проводимости. Количество электронных состояний, соответствующих интервалу энергий между ε и ε + δε, для малых δε оказывается пропорциональным ширине этого интервала δε. Таким образом, его можно обозначить как ρ (ε) δε, где ρ (ε) – некоторая функция энергии, называемая плотностью состояний.

В нормальном металле плотность состояний в такой зоне изменяется непрерывно. Каждое из этих состояний может быть занято электроном или оставаться свободным. При температуре T = 0 K все низкоэнергетические состояния, с энергиями ε меньше определенного значения ε Ф (энергия Ферми), заняты электронами, в то время как состояния с энергиями ε > ε Ф пусты (илл. a). В сверхпроводнике же при низких температурах в зависимости от плотности состояний около энергии Ферми появляется энергетическая щель (илл. b). И этот факт совершенно необычен! Действительно, в физике твердого тела хорошо известно, что если энергия Ферми системы электронов приходится в энергетическом спектре на щель, а не на зону проводимости, то это вещество является диэлектриком (см. главу 28, «Фотоэлектрический эффект и солнечные батареи»). В случае же сверхпроводника все происходит наоборот: при открытии около уровня Ферми щели его сопротивление исчезает!

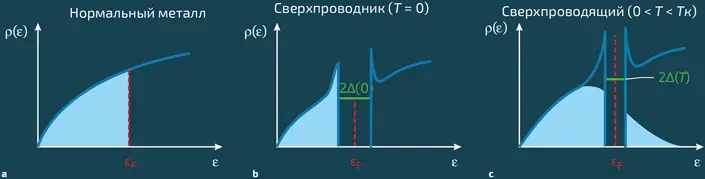
a. Плотность электронных состояний нормального металла в районе энергии Ферми. Состояния заштрихованной области при нулевой температуре заняты. b.Плотность состояний сверхпроводника при нулевой температуре. c.Плотность состояний одного и того же сверхпроводника при конечной температуре ниже критической; щель сужается, и электроны появляются и в зоне проводимости. (Пропорции не соблюдены, Δ обычно намного меньше энергии Ферми Ɛ Ф )

Каков же размер такой пары? Давайте его оценим. Скорости электронов в корке апельсина определяются величиной ε Ф и оказываются весьма большими: v Ф = 10 6м/с. По теории размерности из v Ф и дебаевской частоты W D = 10 12с –1можно составить характерную длину v Ф /W D . Таким образом, два электрона с противоположными скоростями, близкими к v Ф , образуют куперовскую пару размером порядка микрометра. Поскольку это расстояние велико по сравнению с межатомным, то, как мы и предположили выше, кулоновское отталкивание между двумя электронами действительно сильно экранируется другими электронами и ионами решетки.

Согласно метафоре, предложенной Шриффером, куперовская пара должна представляться не образованной из электронов двойной звездой, а скорее как пара пришедших вместе на дискотеку танцоров, которые то сближаются, то удаляются друг от друга, но все же танцуют вместе, независимо от того, разделены ли они в данный момент другими танцорами или нет.

Чтобы «разорвать» куперовскую пару на два составляющих ее электрона, необходимо затратить некоторую энергию Δ, называемую сверхпроводящей щелью. По мере того как сверхпроводник нагревается, щель сужается и все большее количество пар разрывается. Щель в конечном итоге обращается в ноль при достижении критической температуры, и сверхпроводящее состояние исчезает, электронам больше энергетически «невыгодно» образовывать пары (см. врезку «Плотность электронных состояний в металле… который становится сверхпроводником»).

Таким образом, теория БКШ дала долгожданное объяснение микроскопического механизма явления сверхпроводимости. Кроме того, она обосновала и позволила вычислить значения коэффициентов в феноменологических уравнениях Гинзбурга – Ландау, которые и по сегодняшний день остаются весьма удобным и универсальным аппаратом описания явления сверхпроводимости.