Ричард Фейнман - Фейнмановские лекции по физике. Современная наука о природе [litres]

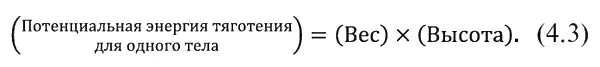
Не правда ли, очень красивое рассуждение? Вопрос только в том, справедливо ли оно. (Ведь, в конце концов, природа не обязана следовать нашим рассуждениям.) Например, не исключено, что в действительности вечное движение возможно. Или другие предположения ошибочны. Или мы просмотрели что-то в своих рассуждениях. Поэтому их непременно нужно проверить. И вот – справедливость их подтверждает опыт.

Потенциальная энергия – это общее название для энергии, связанной с расположением по отношению к чему-либо. В данном частном случае это – потенциальная энергия тяготения . Если же производится работа против электрических сил, а не сил тяготения, если мы «поднимаем» заряды «над» другими зарядами с помощью многочисленных рычагов, тогда запас энергии именуется электрической потенциальной энергией . Общий принцип состоит в том, что изменения энергии равны силе, умноженной на то расстояние, на котором она действует:

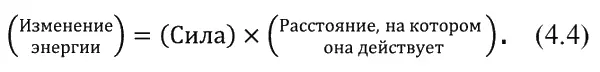
По мере чтения курса мы еще не раз будем возвращаться к другим видам потенциальной энергии.

Принцип сохранения энергии во многих обстоятельствах оказывается очень полезен при предсказании того, что может произойти. В средней школе мы учили немало правил о блоках и рычагах. Мы можем теперь убедиться, что все эти «законы» сводятся к одному , и нет нужды запоминать 75 правил. Вот вам простой пример: наклонная плоскость. Пусть это треугольник со сторонами 3, 4, 5 (фиг. 4.3).

Подвесим к блочку груз весом 1 кг и положим его на плоскость, а с другой стороны подвесим груз W.

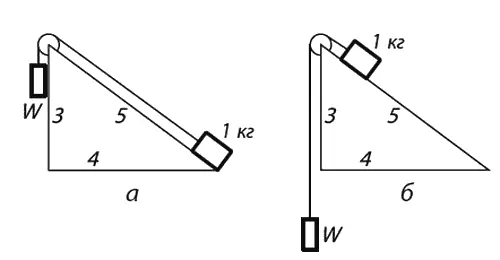
Фиг. 4.3. Наклонная плоскость.

Мы хотим знать, какова должна быть тяжесть W , чтобы уравновесить груз 1 кг . Рассуждаем так. Если грузы W и 1 кг уравновешены, то это – обратимое состояние, и веревку можно двигать вверх-вниз. Пусть же вначале (фиг. 4.3, а ) 1 кг находится внизу плоскости, а груз W – наверху. Когда W соскользнет вниз, груз 1 кг окажется наверху, a W опустится на длину склона (фиг. 4.3, б ), т. е. на 5 м . Но ведь мы подняли 1 кг только на высоту 3 м , хотя опустили W на 5 м . Значит, W = 3/ 5 кг . Заметьте, что этот ловкий вывод получен не из разложения сил, а из сохранения энергии . Ловкость, впрочем, относительна. Существует другой вывод, куда красивее. Он придуман Стевином и даже высечен на его надгробии. Фиг. 4.4 объясняет, почему должно получиться 3/ 5 кг : цепь не вращается и нижняя ее часть уравновешена сама собой, значит сила тяги пяти звеньев с одной стороны должна уравнять силу тяги трех звеньев с другой (по длине сторон).

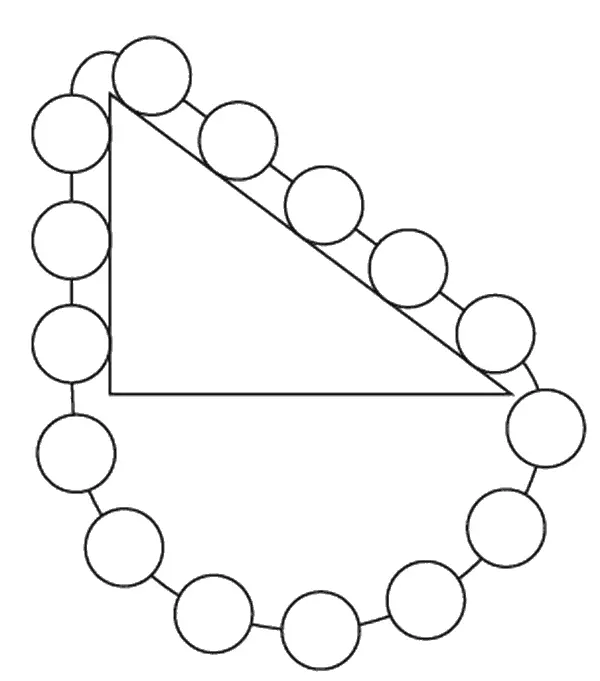
Фиг. 4.4. Это выгравировано на надгробии Стевина.

Глядя на диаграмму, становится очевидно, что W = 3/ 5 кг. (Неплохо было бы, если бы когда-нибудь что-нибудь подобное высекли и на вашем надгробном камне.)

А вот задача посложнее: домкрат, показанный на фиг. 4.5.

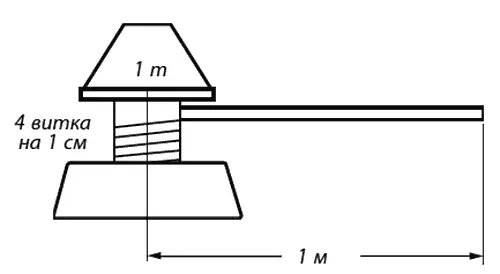
Фиг. 4.5. Домкрат.

Посмотрим, как в таком случае применять этот принцип. Для вращения домкрата служит ручка длиной 1 м , а нарезка винта имеет 4 витка на 1 см . Какую силу нужно приложить к ручке, чтобы поднять 1 m ? Желая поднять 1 т на 1 см , мы должны обойти домкрат четырежды, каждый раз делая по 6,28 м (2 πr ), а всего 25,12 м . Используя различные блоки и т. п., мы действительно можем поднять 1 т с помощью неизвестного груза W , приложенного к концу ручки. Ясно, что W равно примерно 400 г . Это – следствие сохранения энергии.

И еще более сложный пример (фиг. 4.6).

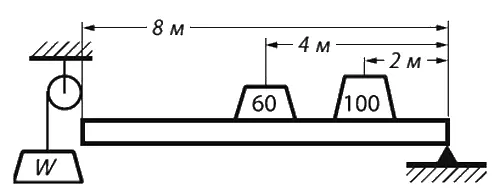
Фиг. 4.6. Нагруженный стержень, подпертый с одного конца.

Подопрем один конец стержня (или рейки) длиной 8 м . Посредине рейки поместим груз весом 60 кг , а в 2 м от подпорки – груз весом 100 кг . Сколько надо силы, чтобы удержать рейку за другой конец в равновесии, пренебрегая ее весом? Пусть мы прикрепили блок и перекинули через него веревку, привязав ее к концу рейки. Каков же должен быть вес W , уравновешивающий стержень? Представим, что вес опустился на произвольное расстояние (для простоты пусть это будет 4 см );на сколько тогда поднимутся наши два груза? Середина рейки на 2 см , а второй груз (он лежит на четверти длины рейки) на 1 см . Значит, в согласии с правилом, что сумма весов, умноженных на высоты, не меняется, мы должны написать: вес W на 4 см вниз плюс 60 кг на 2 см вверх плюс 100 кг на 1 см вверх, что после сложения должно дать нуль:

−4 W + 2 × 60 + 1 × 100 = 0, W = 55 кг. (4.5)

Выходит, чтобы удержать рейку, хватит 55 кг . Таким же путем можно разработать законы «равновесия» – статику сложных мостовых сооружений и т. д. Такой подход именуют принципом виртуальной (т. е. возможной или воображаемой) работы , потому что для его применения мы обязаны представить себе , что наша система чуть сдвинулась, даже если она в действительности не двигалась или вовсе не способна двигаться. Мы используем небольшие воображаемые движения, чтобы применить принцип сохранения энергии.

Чтобы рассказать о другом виде энергии, рассмотрим маятник (фиг. 4.7). Отведем его в сторону и затем отпустим. Он начнет качаться взад и вперед. Двигаясь от края к середине, он теряет высоту. Куда же девается потенциальная энергия? Когда он опускается до самого низа, энергия тяготения пропадает, однако он вновь взбирается вверх. Выходит, что энергия тяготения должна превращаться в другую форму. Ясно, что способность взбираться наверх остается у маятника благодаря тому, что он движется; значит, в наинизшей точке качания энергия тяготения переходит в другой вид энергии.

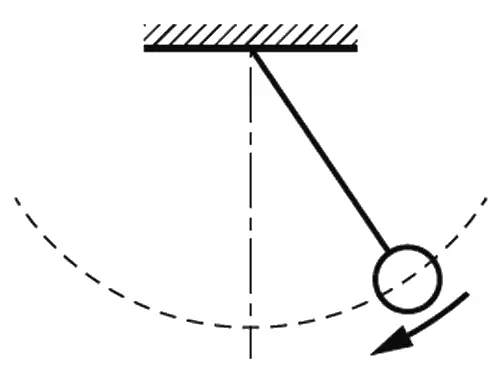
Фиг. 4.7. Маятник.

Мы должны получить формулу для энергии движения. Вспоминая наши рассуждения о необратимых машинах, мы легко поймем, что, двигаясь мимо наинизшей точки, маятник должен обладать некоторым количеством энергии, которая позволит ему подняться на определенную высоту, и при этом независимо от механизма подъема или пути подъема. Возникает формула, выражающая равноценность обоих видов энергии, подобная той, которую писала мама, подсчитывая кубики. Получается другая форма представления энергии. Легко понять, какой она должна быть. Кинетическая энергия внизу равна весу, умноженному на высоту, на которую этот вес может подняться из-за своей скорости: